Question

In $\Delta ABC,AB=AC\ and \ D$ is a point on side AC such that AD = BD = BC. Show that: $\angle ADB=108{}^\circ $.

Answer 1

Hint: To show that $\angle ADB=108{}^\circ $, we will first find $\angle ABC$ and then we will try to find out the angle $\angle ABD$. With the help of this and by using the property that the sum of all sides of a triangle is $180{}^\circ $, we will show that $\angle ABD$ in this $\Delta ABC$ is of $108{}^\circ $.

Complete step-by-step answer:
It is given in the question that ABC is a triangle in which side AB = side AC. D is a point on side AC such that AD = BC. We have to show that $\angle ADB=108{}^\circ $.
Let us consider the given conditions and draw a diagram of triangle ABC.

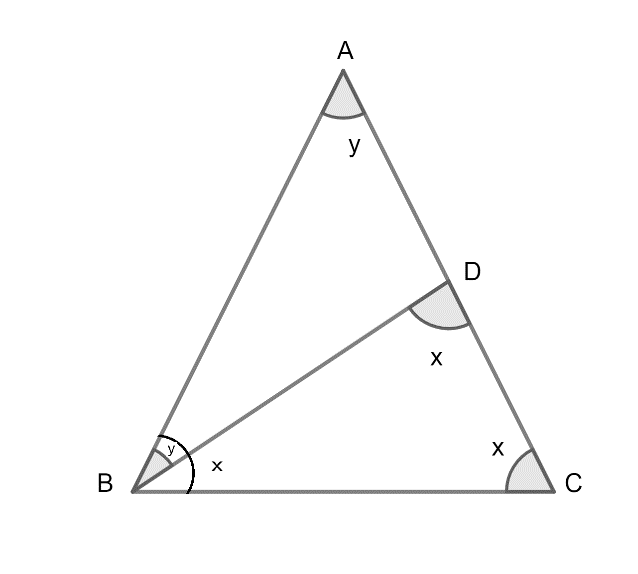
Now, in triangle ABC we have the side AB = the side AC as it is given in question. So, we know that the angles opposite to the equal sides of a triangle are equal. Thus, from this property of the triangle, we get $\angle ABC=\angle ACB$.
Let us assume that $\angle ABC=\angle ACB=x................\left( 1 \right)$
Now, in triangle BDC, we have side BD = BC as it is given in question. Also, we know that angles opposite to the equal sides of a triangle are equal. Thus, from this property of the triangle, we get $\angle BDC=\angle DCB$.
As, we have already assumed that $\angle ACB=x$, we get that $\angle BDC=\angle DCB=x..................\left( 2 \right)$
Let us consider triangle ADB. It is given in the question that sides AD and BD are equal. Therefore, we can say that the opposite angles will also be equal, i.e. $\angle BAD=\angle ABD$.
So, let us assume that $\angle BAD=\angle ABD=y...............\left( 3 \right)$
We know that the sum of all the angles of a triangle is $180{}^\circ $. Keeping this in property of triangle in mind, if we observe $\Delta ABC$, we get,
\[\angle ABC+\angle BCA+\angle CAB=180{}^\circ ..................\left( 4 \right)\]
We know that \[\angle ABC=x\And \angle BCA=x\ also\ \angle CAB=y\]. So, putting the value of \[\angle ABC\ as\ x,\angle BCA\ as\ x\ and\ \angle CAB=y\] in equation (4), we get,
$\begin{align}
  & x+x+y=180{}^\circ \\
 & \Rightarrow 2x+y=180{}^\circ ..................\left( 5 \right) \\
\end{align}$
Now, in triangle ABD, BDC is an exterior angle, and we know that exterior angle is equal to the sum of two opposite interior angles. From this in $\Delta ABD$, we get,
$\angle ABD+\angle BAD=\angle BDC..............\left( 6 \right)$
Also, we know that \[\angle ABD=y\ and\ \angle BDC=x\ and\ \angle BAD=y\]. So, on putting the value of\[\angle ABD,\angle BDC\ as\ x\ and\ \angle BAD=y\]in equation (6), we get;
\[\begin{align}
  & \angle ABD+\angle BAD=\angle BDC \\
 & \Rightarrow y+y=x \\
 & \Rightarrow x=2y......................\left( 7 \right) \\
\end{align}\]
Or, we can write y in terms of x as $y=\dfrac{x}{2}$ . On substituting the value of y as $y=\dfrac{x}{2}$in equation (5), we get;
$\begin{align}
  & 2x+\left( \dfrac{x}{2} \right)=180 \\
 & \Rightarrow \dfrac{4x+x}{2}=180 \\
 & \Rightarrow \dfrac{5x}{2}=180 \\
 & \Rightarrow 5x=180\times 2 \\
 & \Rightarrow 5x=360 \\
 & \Rightarrow x=\dfrac{360}{5} \\
 & \Rightarrow x=72 \\
\end{align}$
Thus, we get x = 72. Now as we know that $\dfrac{x}{2}=y$, so $2y=x$. We can get the value of y as,
$\begin{align}
  & \Rightarrow \dfrac{x}{2}=y \\
 & \Rightarrow \dfrac{72}{2}=y \\
 & \Rightarrow y=36{}^\circ \\
\end{align}$
Now, again let us consider triangle ADB. As, we have already discussed that the sum of all the three sides of a triangle is $180{}^\circ $.
Thus, $\angle ABD+\angle BDA+\angle DAB=180{}^\circ $
 $\begin{align}
  & \Rightarrow y+y+\angle ADB=180{}^\circ \\
 & \Rightarrow 2y+\angle ADB=180{}^\circ ...................\left( 8 \right) \\
\end{align}$
We know that $y=36{}^\circ $. So, on putting the value of $y\ as\ 36{}^\circ $ in equation (8) we get;
$\begin{align}
  & \Rightarrow 2\left( 36{}^\circ \right)+\angle ADB=180{}^\circ \\
 & \Rightarrow 72{}^\circ +\angle ADB=180{}^\circ \\
 & \Rightarrow \angle ADB=180{}^\circ -72{}^\circ \\
 & \Rightarrow \angle ADB=108{}^\circ \\
\end{align}$
Thus, we get $\angle ADB=108{}^\circ $.
Hence, proved.

Note: We can solve this question in just a few steps, if we know the basic concepts of angles between lines and properties of triangles. In the last part of the solution we have considered the $\Delta ADB$ to find the value of $\angle ADB$, which consumes time. So, instead of this we can have the concept of linear pair as we know that any side of a polygon is a line and angle made on line is always$180{}^\circ $. Thus, we get $\angle CDB+\angle BDA=180{}^\circ $ as both of them forming linear pairs. We have already calculated that $\angle CDB=72{}^\circ $. So, from this we directly get $\angle BDA=180{}^\circ -72{}^\circ $
$\Rightarrow \angle BDA=108{}^\circ $.