
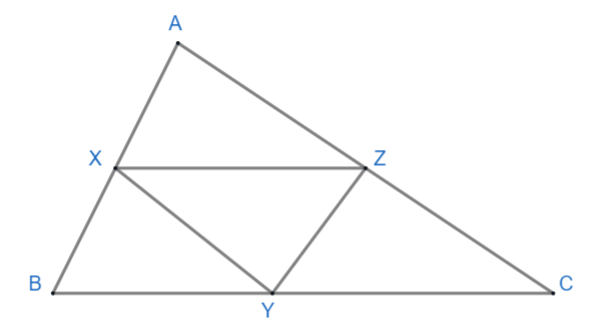
In $ \Delta ABC $ , X, Y and Z are midpoint of side AB, side BC and side AC respectively. AB = 5cm, AC = 9cm and BC = 11cm. Then find XZ.
\[\begin{align}
& A.2.7cm \\
& B.5.5cm \\
& C.8.3cm \\
& D.9.5cm \\
\end{align}\]

Answer
574.2k+ views
Hint: In this question, we are given the length of the three sides of a triangle $ \Delta ABC $. We are also given their midpoint X, Y, and Z. We need to find the length of XZ. For this, we will use the midpoint theorem according to which the line segments connecting the midpoint of two sides of a triangle is parallel to the third side and is equal to one half of the third side.
Here we are given the triangle ABC in which X, Y, and Z are the midpoints of side AB, BC, and AC respectively. Our diagram looks like this,
Complete step by step answer:
Here AB = 5cm, AC = 9cm and BC = 11cm. We need to find XZ. As we know from the diagram, since X is the midpoint of AB and Z is the midpoint of AC, so we can apply the midpoint theorem for the line joining points X and Z i.e. the line XZ.
According to the midpoint theorem, the line segment connecting the midpoint of two sides of a triangle is parallel to the third side and is equal to half of the third side, so in $ \Delta ABC $ where X is the midpoint of AB and Z is the midpoint of AC, XZ is the line which should be parallel and equal to half of the third side of the triangle i.e. BC. Therefore we can say that XZ is parallel to BC and equal to half of BC.
$ \therefore XZ=\dfrac{1}{2}BC $ .
We know that BC = 11cm. Therefore, $ XZ=\dfrac{1}{2}\times 11cm=5.5cm $ .
Hence the required length of XZ is 5.5cm.
Therefore, option B is the correct answer.
Note:
Students should carefully apply the midpoint theorem in any triangle. Note that, points should be midpoint for both sides, not just one. Take care of units while writing the final answer. Students should keep in mind the midpoint theorem as we as the converse of it.
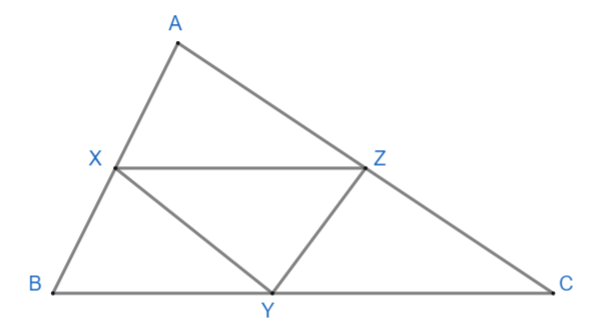
Here we are given the triangle ABC in which X, Y, and Z are the midpoints of side AB, BC, and AC respectively. Our diagram looks like this,

Complete step by step answer:
Here AB = 5cm, AC = 9cm and BC = 11cm. We need to find XZ. As we know from the diagram, since X is the midpoint of AB and Z is the midpoint of AC, so we can apply the midpoint theorem for the line joining points X and Z i.e. the line XZ.
According to the midpoint theorem, the line segment connecting the midpoint of two sides of a triangle is parallel to the third side and is equal to half of the third side, so in $ \Delta ABC $ where X is the midpoint of AB and Z is the midpoint of AC, XZ is the line which should be parallel and equal to half of the third side of the triangle i.e. BC. Therefore we can say that XZ is parallel to BC and equal to half of BC.
$ \therefore XZ=\dfrac{1}{2}BC $ .
We know that BC = 11cm. Therefore, $ XZ=\dfrac{1}{2}\times 11cm=5.5cm $ .
Hence the required length of XZ is 5.5cm.
Therefore, option B is the correct answer.
Note:
Students should carefully apply the midpoint theorem in any triangle. Note that, points should be midpoint for both sides, not just one. Take care of units while writing the final answer. Students should keep in mind the midpoint theorem as we as the converse of it.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Which country won the ICC Men's ODI World Cup in 2023?

In cricket, how many legal balls are there in a standard over?

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

What does "powerplay" mean in limited-overs cricket?

What is the "Powerplay" in T20 cricket?




