Question

: In $ \Delta ABC $, we have $ \angle A=70{}^\circ ,\angle B=30{}^\circ $ and $ \angle C=80{}^\circ $. Which of the following is correct?
[a] $ AB > BC < AC $
[b] $ AB < BC > AC $
[c] $ AB > BC > AC $
[d] $ AB < BC < AC $

Answer 1

Hint: Use the fact that in a triangle the greater angle has a longer opposite side. Hence determine the order of the sides with respect to each other.

Complete step-by-step answer:

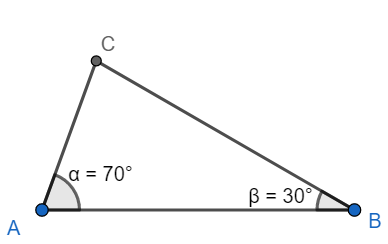
In triangle ABC, we have $ \angle A=70{}^\circ $ and $ \angle B=30{}^\circ $

Hence, we have $ \angle A > \angle B $

We know that in a triangle a greater angle is opposite to the larger side.

Now, we have AC is opposite to $ \angle B $ and BC is opposite to $ \angle A $

Hence, we have $ BC > AC \text{ }\left( i \right) $.

Similarly, we have $ \angle A=70{}^\circ $ and $ \angle C=80{}^\circ $

Hence, we have $ \angle A < \angle C $

We know that in a triangle a greater angle is opposite to the larger side.

Now, we have BC is opposite to $\angle A$ and AB is opposite to $ \angle C $. Hence, we have

$ AB > AC \text{ }\left( ii \right) $

Combining inequalities (i) and (ii), we get

$ AB > BC > AC $

Hence option [c] is correct.

Option [a] is incorrect since $ BC > AC $

Option [b] is incorrect since $ AB > BC $

Option [d] is incorrect since $ AB > BC $.

Note: [i] In a triangle longer side has greater angle

Proof:

Consider a triangle ABC, with $ AB > AC $

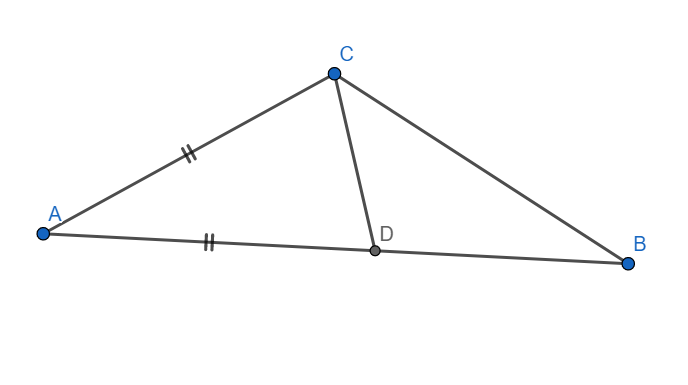
Mark point D on AB such that AD = AC.

Since in a triangle equal angles have equal opposite sides, we have

$ \angle ACD = \angle ADC $

By Linear pair axiom, we have

$ \angle CDB=180{}^\circ - \angle CDA $

Also, by angle sum property of a triangle, we have

$ \angle B=180{}^\circ - \left( \angle CDB + \angle DCB \right)=180{}^\circ - \left( 180{}^\circ - \angle CDA+\angle DCB \right)=\angle CDA-\angle DCB \left( i \right) $

Also, we have

$ \angle C= \angle DCB + \angle DCA $

Since $ \angle DCA = \angle CDA $, we have

$ \angle C= \angle DCB + \angle CDA \text{ } \left( ii \right) $

Subtracting equation (ii) from equation (i), we get

$ \angle C- \angle A = 2 \angle DCB >0 $

Hence, we have

$ \angle C > \angle A$

Q.E.D

[ii] In a triangle a greater angle has a larger side.

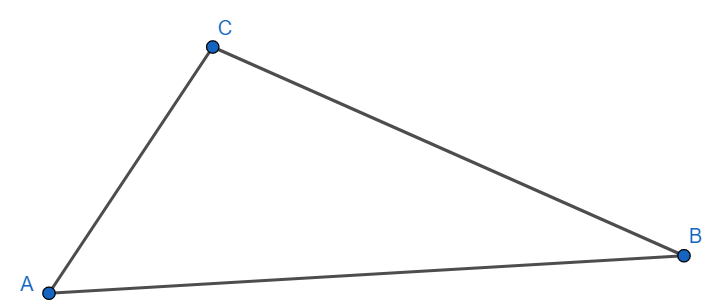
We have $ \angle C > \angle A$

To prove $AB>BC$

Proof: Suppose not. Suppose $ AB < BC $

Hence from the above proved result, we have $ \angle C < \angle A $.

A contradiction.

Hence our assumption is incorrect.

Hence $ AB>BC $

Q.E.D