Question

In $\Delta $ABC and $\Delta $DEF, AB = DE, BC = EF and $\angle \text{B}$=$\angle \text{E}$. If the perimeter of $\Delta $ABC is 20, then the perimeter of $\Delta $DEF is

Answer 1

Hint: Here, we need to first draw both the triangles mentioned according to the given data. Next step is to prove the similarity of both the triangles with the help of side – angle – side test. Finally, if the triangles are similar to each other, the perimeter will also be equal to each other.

Complete step-by-step answer:
Let us first draw the triangles ABC and DEF, the conditions are AB = DE, BC = EF and $\angle \text{B}$=$\angle \text{E}$.

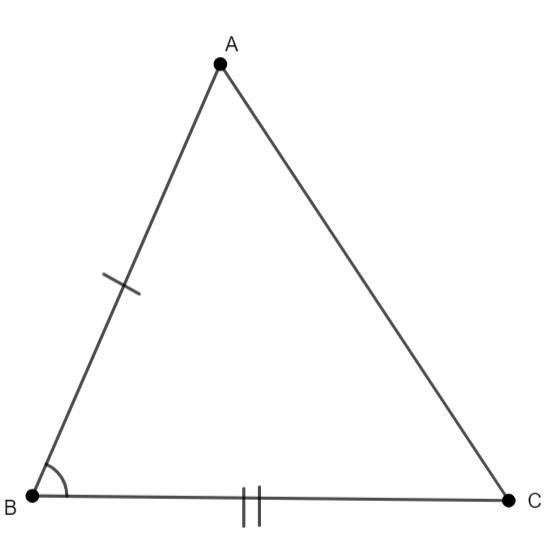
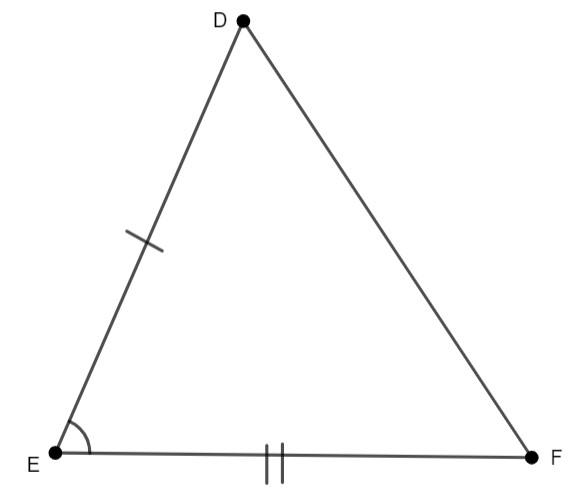
From the diagram drawn we can see that they both look identical. Let us find the relativity between the both the triangles ABC and DEF
Here, we have first AB = DE, this shows that one of the sides of both triangles are congruent.
Next, we have BC = EF, this shows that the second side of both the triangles are congruent.
Now, it is also given that $\angle \text{B}$=$\angle \text{E}$, this indicates that one of the angles in both the triangles are congruent.
Therefore, $\Delta $ABC $\sim $$\Delta $DEF (By side – angle – side test)
We proved that both the triangles are similar to each other or are congruent to each other.
Now, if $\Delta $ABC, has a perimeter of 20 units, since both the triangles are similar to each other, the perimeter of the $\Delta $DEF is also 20 units.
Hence, the perimeter of the $\Delta $DEF is 20 units.

Note: In this question, even if any of the three conditions were changed, the similarity would have not occurred. There are other similar tests like angle-angle, side-side-side, hypotenuse leg tests which are also used to prove the similarity between the triangles.