Question

In $\Delta {\text{ABC}}$, AB$ = 6\sqrt 3 $, AC$ = 12{\text{ cm}}$, BC$ = 6{\text{ cm}}$. Find the measure of $\angle {\text{A}}$.
A) $30^\circ $
B) $60^\circ $
C) $90^\circ $
D) $45^\circ $

Answer 1

Hint: First analyze that the given triangle is a right-angled triangle or not using the Pythagoras theorem and then apply the trigonometric ratio for angle A to get the desired result.

Complete step by step solution:
It is given in the problem that, AB$ = 6\sqrt 3 $, AC$ = 12{\text{ cm}}$, BC$ = 6{\text{ cm}}$ in the triangle ABC.
We have to find the measure of angle $A$.
In this problem, we can use the Pythagoras theorem that states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides named base and perpendicular of the triangle.
First, do the square of all dimensions of sides of triangles and see if the triangle is a right angle or any other. In a right-angled triangle, the hypotenuse is the largest side.
Take a look at the figure of the right-angled triangle ABC,

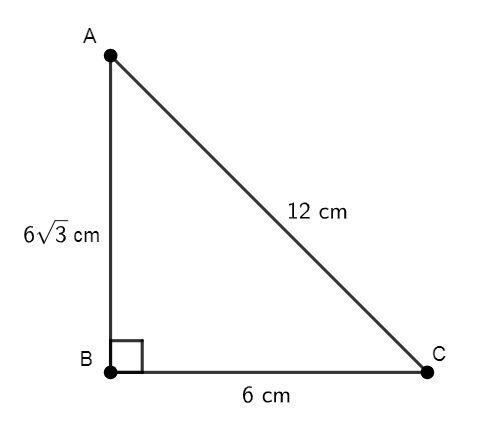
The side in front of the right angle is called as hypotenuse, BC is the base of the triangle and AB is the perpendicular of the triangle
Now, find the square of the side lengths of the triangle given above in the figure.
${\left( {AB} \right)^2} = {\left( {12} \right)^2} = 144$
${\left( {BC} \right)^2} = {\left( 6 \right)^2} = 36$
${\left( {AB} \right)^2} = {\left( {6\sqrt 3 } \right)^2} = 108$
Now, according to the Pythagoras theorem,
${\left( {AB} \right)^2} + {\left( {BC} \right)^2} = {\left( {AC} \right)^2}$
On substituting the values, we can see that it holds the Pythagoras theorem, thus it gives the conclusion that the given triangle is a right-angles triangle.
Since the given triangle is a right angles triangle so we can apply the trigonometric ratio in the triangle ABC.
According to the trigonometric ratio, the tangent of angle A is the ratio of the perpendicular and the base of the triangle ABC. That is,
$\dfrac{{AB}}{{BC}} = \tan {\text{A}}$
Now, we substitute the values of AB and BC.
$\dfrac{{6\sqrt 3 }}{6} = \tan {\text{A}}$
$ \Rightarrow \tan {\text{A = }}\sqrt 3 $
We know that:
$\tan 30^\circ = \sqrt 3 $
So, we have
\[{\text{tanA}} = \tan 30^\circ \]
$A = 30^\circ $

$\therefore$ The measure of$\angle {\text{A}}=30^\circ$. Hence, option A is correct.

Note:
For any right-angled triangle, the side in front of the right angle is the hypotenuse, the side in front of the given angle is perpendicular and the adjacent side of the angle is the base of the triangle.