Question

In any $\vartriangle $ABC If aCosB = bCosA then the triangle is
A) Equilateral triangle
B) Isosceles triangle
C) Scalene triangle
D) Right angle triangle

Answer 1

Hint: Here, we will use ‘The Law of Cosines’ (${a^2} = {b^2} + {c^2} - 2bc$$\cos A$ and ${b^2} = {c^2} + {a^2} - 2ac$$\cos B$) to find the value of aCosB and bCosA from the theorem and put the values in the question given above. We are using this theorem because the cosine rule relates all 3 sides of a triangle with an angle of a triangle. In the statement, we have given a combination of sides and angles. So, it is easy to use this law to prove the given statement.

Complete step by step solution:
Given: aCosB = bCosA ………. (1)
In any $\vartriangle $ ABC, we have
The sides BC, CA and AB are opposite to the angles A, B and C respectively. The side BC is denoted by ‘a’, the side AC is denoted by ‘b’ and the side AB is denoted by ‘c’.

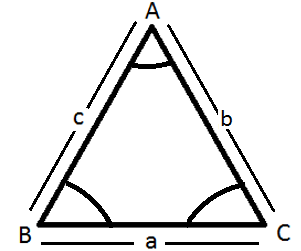
Theorem 1: ${a^2} = {b^2} + {c^2} - 2bc$$\cos A$
From this equation we will find the value of bCosA
$2bc$$\cos A$ = \[{b^2} + {c^2} - {a^2}\]
$ \Rightarrow $ $b\cos A = \dfrac{{\left( {{b^2} + {c^2} - {a^2}} \right)}}{{2c}}$................(2)
Now
Theorem 2:
${b^2} = {c^2} + {a^2} - 2ac$$\cos B$
$ \Rightarrow $ $2ac$$\cos B$ = \[{c^2} + {a^2} - {b^2}\]
$ \Rightarrow $ $a\cos B = \dfrac{{\left( {{c^2} + {a^2} - {b^2}} \right)}}{{2c}}$................. (3)
Put the value of (2) and (3) in (1) equation, we get
$ \Rightarrow $ $\dfrac{{\left( {{c^2} + {a^2} - {b^2}} \right)}}{{2c}}$ = $\dfrac{{\left( {{b^2} + {c^2} - {a^2}} \right)}}{{2c}}$
Multiply both sides by 2c because in an equation we can multiply to both sides by the same number.
 $ \Rightarrow $ $\dfrac{{\left( {{c^2} + {a^2} - {b^2}} \right)}}{{2c}} \times 2c$ = $\dfrac{{\left( {{b^2} + {c^2} - {a^2}} \right)}}{{2c}} \times 2c$
Here our purpose is to cancel out 2c which is in the denominator of LHS and RHS, we get
$ \Rightarrow $ \[{c^2} + {a^2} - {b^2}\] = \[{b^2} + {c^2} - {a^2}\]
$ \Rightarrow $ ${c^2} - {c^2} + {a^2} + {a^2} = {b^2} + {b^2}$
$ \Rightarrow $ $2{a^2} = 2{b^2}$
$ \Rightarrow $ ${a^2} = \dfrac{{2{b^2}}}{2}$
$ \Rightarrow $ ${a^2} = {b^2}$
$ \Rightarrow $ a = b (a,b are positive)

\[\therefore \] Two sides of a triangle are equal so the Triangle ABC is an Isosceles triangle

Note:
Alternative method:
We can also apply ‘The LAW OF SINES OR SINE RULE’ (which is equal to \[\]$\dfrac{a}{{\operatorname{Sin} A}} = \dfrac{b}{{\operatorname{Sin} B}} = \dfrac{c}{{\operatorname{Sin} C}}$) to find out the type of triangle. By using this Law, we can find out the value of ‘a’ and ‘b’ and put in the question given above. We will use ‘The Sine Law’ because sine rule is an equation relating the lengths of the sides of a triangle (any shape) to the Sines of its angles. In the statement, we have given a combination of sides and angles.
In any $\vartriangle $ ABC, we have
The sides BC, CA, and AB are opposite to the angles A, B, and C respectively. The side BC is denoted by ‘a’, the side AC is denoted by ‘b’ and the side AB is denoted by ‘c’.

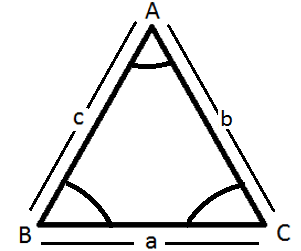
 The LAW OF SINES OR SINE RULE = $\dfrac{a}{{\operatorname{Sin} A}} = \dfrac{b}{{\operatorname{Sin} B}} = \dfrac{c}{{\operatorname{Sin} C}}$
Let, $\dfrac{a}{{\operatorname{Sin} A}} = \dfrac{b}{{\operatorname{Sin} B}} = \dfrac{c}{{\operatorname{Sin} C}}$ = k, where k is a constant
a = k Sin A, b = k Sin B
Put the values of a and b in the equation given in the question
$ \Rightarrow $ aCosB = bCosA
$ \Rightarrow $ k Sin A.Cos B = k Sin B.Cos A
We can cancel ‘k’ from both L.H.S and R.H.S
$ \Rightarrow $ Sin A.Cos B = Sin B.Cos A
$ \Rightarrow $ Sin A.Cos B - Sin B.Cos A = 0 ……….(1)
Here use an identity: $\operatorname{Sin} (\alpha - \beta ) = \operatorname{Sin} \alpha \operatorname{Cos} \beta - \operatorname{Cos} \alpha \operatorname{Sin} \beta $
So, Sin(A-B) = Sin A.Cos B - Sin B.Cos A
$ \Rightarrow $ Sin(A-B) = 0
$ \Rightarrow $ Sin(A-B) is equal to 0 at Sin $0^\circ $, Sin $180^\circ $, Sin$360^\circ $ But, In any triangle the difference between two angles can never $180^\circ $,$360^\circ$
 $\therefore $ Sin(A-B) = Sin $0^\circ $
 $ \Rightarrow $ A-B = 0
 $ \Rightarrow $ A = B
The Converse of the Isosceles Triangle Theorem states: If two angles of a triangle are equal, then sides opposite those angles are equal. So the Triangle ABC is an Isosceles Triangle.