
In an orthorhombic crystal, a lattice plane cuts intercepts in the ratio 1:2:3 along a,b and c axes. Find the miller indices of the plane. Sketch the plane and calculate the interplanar spacing, given that a=1A, b=2A and c=3A.
Answer
587.1k+ views
Hint: We have to calculate Miller indices by taking the reciprocals of intercepts and for calculating the interplanar spacing, we have to use the formula,
$\dfrac{1}{{{d_{hkl}}^2}} = \dfrac{4}{3}\left( {\dfrac{{{h^ + } + hk + {k^2}}}{{{a^2}}}} \right) + \left( {\dfrac{{{l^2}}}{{{c^2}}}} \right)$
Here, h, k, and l are miller indices.
Complete step by step answer:
We know that the orthorhombic crystal system is one of the 7 crystal systems.
Orthorhombic lattices comes from enlarging a cubic lattice along two of its orthogonal pairs by two factors, that leads in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are different.
The intersection of all three bases at 90° angles, so the three lattice vectors remain mutually orthogonal.
We know that Miller indices of a plane are the reciprocals of the intercepts of that corresponding to unit length.
Thus, intercepts are a:b:c=1:2:3.
So let us now take the reciprocals:
$\dfrac{1}{a}:\dfrac{1}{b}:\dfrac{1}{c} = \dfrac{1}{1}:\dfrac{1}{2}:\dfrac{1}{3}$
(or) We can take L.C.M and by taking L.C.M, we get the value of miller indices as 6,3,2.
The value of h is 6.
The value of k is 3.
The value of l is 2.
We can represent the miller indices as $\left( {hkl} \right) = \left( {632} \right)$
Let us now calculate the interplanar spacing for orthorhombic crystals.
$\dfrac{1}{{{d_{hkl}}^2}} = \dfrac{4}{3}\left( {\dfrac{{{h^ + } + hk + {k^2}}}{{{a^2}}}} \right) + \left( {\dfrac{{{l^2}}}{{{c^2}}}} \right)$
Let us now substitute the values of a, c, h, k, and l to calculate the interplanar spacing.
$\dfrac{1}{{{d_{hkl}}^2}} = \dfrac{4}{3}\left( {\dfrac{{{{\left( 6 \right)}^2} + \left( 6 \right)\left( 2 \right) + {{\left( 2 \right)}^2}}}{{{{\left( 1 \right)}^2}}}} \right) + \left( {\dfrac{{{{\left( 2 \right)}^2}}}{{{{\left( 3 \right)}^2}}}} \right)$
$ \Rightarrow $$\dfrac{1}{{{d_{hkl}}^2}} = \dfrac{{760}}{9}$
$ \Rightarrow $${d_{hkl}}^2 = \dfrac{9}{{760}}$
$ \Rightarrow $${d_{hkl}} = \dfrac{3}{{\sqrt {760} }}$
The inter-planar spacing is $\dfrac{3}{{\sqrt {760} }}$.
The plane is sketched as,
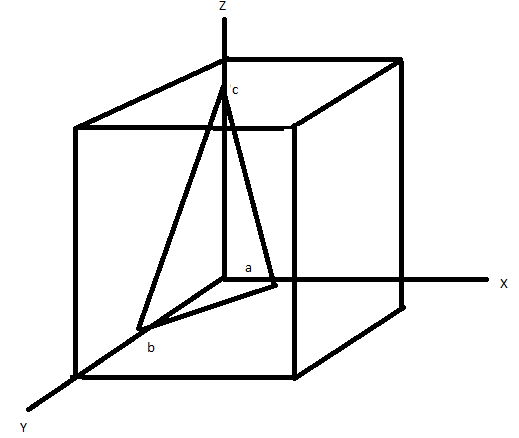
Note:
We have to know that in two dimensions there are two orthorhombic Bravais lattices: primitive rectangular and centered rectangular. In three dimensions, primitive orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic are the four orthorhombic Bravais lattices.
$\dfrac{1}{{{d_{hkl}}^2}} = \dfrac{4}{3}\left( {\dfrac{{{h^ + } + hk + {k^2}}}{{{a^2}}}} \right) + \left( {\dfrac{{{l^2}}}{{{c^2}}}} \right)$
Here, h, k, and l are miller indices.
Complete step by step answer:
We know that the orthorhombic crystal system is one of the 7 crystal systems.
Orthorhombic lattices comes from enlarging a cubic lattice along two of its orthogonal pairs by two factors, that leads in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are different.
The intersection of all three bases at 90° angles, so the three lattice vectors remain mutually orthogonal.
We know that Miller indices of a plane are the reciprocals of the intercepts of that corresponding to unit length.
Thus, intercepts are a:b:c=1:2:3.
So let us now take the reciprocals:
$\dfrac{1}{a}:\dfrac{1}{b}:\dfrac{1}{c} = \dfrac{1}{1}:\dfrac{1}{2}:\dfrac{1}{3}$
(or) We can take L.C.M and by taking L.C.M, we get the value of miller indices as 6,3,2.
The value of h is 6.
The value of k is 3.
The value of l is 2.
We can represent the miller indices as $\left( {hkl} \right) = \left( {632} \right)$
Let us now calculate the interplanar spacing for orthorhombic crystals.
$\dfrac{1}{{{d_{hkl}}^2}} = \dfrac{4}{3}\left( {\dfrac{{{h^ + } + hk + {k^2}}}{{{a^2}}}} \right) + \left( {\dfrac{{{l^2}}}{{{c^2}}}} \right)$
Let us now substitute the values of a, c, h, k, and l to calculate the interplanar spacing.
$\dfrac{1}{{{d_{hkl}}^2}} = \dfrac{4}{3}\left( {\dfrac{{{{\left( 6 \right)}^2} + \left( 6 \right)\left( 2 \right) + {{\left( 2 \right)}^2}}}{{{{\left( 1 \right)}^2}}}} \right) + \left( {\dfrac{{{{\left( 2 \right)}^2}}}{{{{\left( 3 \right)}^2}}}} \right)$
$ \Rightarrow $$\dfrac{1}{{{d_{hkl}}^2}} = \dfrac{{760}}{9}$
$ \Rightarrow $${d_{hkl}}^2 = \dfrac{9}{{760}}$
$ \Rightarrow $${d_{hkl}} = \dfrac{3}{{\sqrt {760} }}$
The inter-planar spacing is $\dfrac{3}{{\sqrt {760} }}$.
The plane is sketched as,

Note:
We have to know that in two dimensions there are two orthorhombic Bravais lattices: primitive rectangular and centered rectangular. In three dimensions, primitive orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic are the four orthorhombic Bravais lattices.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

Name the part of the brain responsible for the precision class 11 biology CBSE

The growth of tendril in pea plants is due to AEffect class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




