Question

In an isosceles triangle ABC, with $AB=AC$, the bisectors of $\angle B$ and $\angle C$ intersect each other at $O$. Join $A$ to $O$. Show that: \[\]
(i) $OB=OC$\[\]
(ii)$AO$ Bisects $\angle A$ \[\]

Answer 1

Hint: We use the theorems that the angle opposite to equal sides will be equal and sides opposite to equal angles will be equal to get $\angle ABC=\angle ACB$ and then prove $OB=OC$. We use Side-Side-Side congruence of triangles for triangles ABO and ACO to prove $\angle BAO=\angle CAO$ which makes $AO$ the bisector of $\angle A$.

Complete step-by-step solution
We know that if measures of two angles in a triangle are equal then the length of their opposite sides are equal. Its converse is also true which means if the lengths of two sides of a triangle are equal then the measures of their opposite angles are equal.
We are given in the question that an isosceles triangle ABC with equal sides $AB=AC$. We are also given the bisectors of $\angle B$ and $\angle C$ intersect each other$O$.\[\]

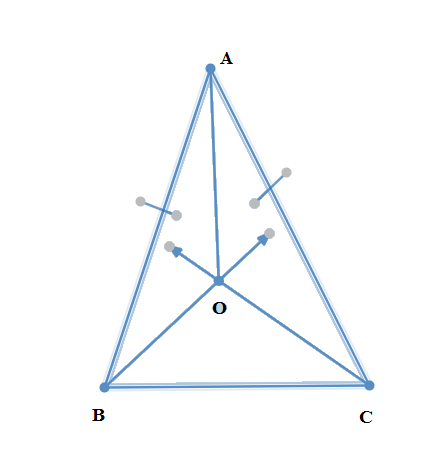
(i) We are asked to prove $OB=OC$. Let us consider the triangle ABC which has equal sides$AB=AC$. So now their opposite angles will be equal which are
\[\angle ABC=\angle ACB....\left( 1 \right)\]
We have from the figure,
\[\begin{align}
  & \angle ABC=\angle ABO+\angle CBO.....\left( 2 \right) \\
 & \angle ACB=\angle ACO+\angle BCO.....\left( 3 \right) \\
\end{align}\]
We have $\overrightarrow{BO}$ as a bisector of $\angle B$ and $\overrightarrow{OC}$ as a bisector of angle$\angle C$. The bisector of angles divides the angle into two equal angles. The bisector $\overrightarrow{BO}$ divides $\angle B=\angle ABC$ into two equal angles which are $\angle ABO=\angle CBO$. The bisector $\overrightarrow{CO}$ divides $\angle C=\angle ACB$ into two equal angles which are $\angle ACO=\angle BCO$. So we have from (1), (2) and (3)
\[\begin{align}
  & \Rightarrow \angle ABC=\angle ACB \\
 & \Rightarrow \angle ABO+\angle CBO=\angle ACO+\angle BCO \\
 & \Rightarrow \angle CBO+\angle CBO=\angle BCO+\angle BCO \\
 & \Rightarrow 2\angle CBO=2\angle BCO \\
 & \Rightarrow \angle CBO=\angle BCO \\
\end{align}\]
Let us consider the triangle OBC. We have equal angles $\angle CBO=\angle BCO$. SO their opposite sides will be equal which are $OC=OB\Rightarrow OB=OC$. Hence it is proved. \[\]
(ii) We are asked to prove $AO$ Bisects $\angle A$ which means $AO$ divides $\angle A=\angle BAC$ into two equal angles$\angle BAO=\angle CAO$.
We observe the triangles $\Delta ABO $ and $\Delta ACO$. We are given $AB=AC$. We have proved in part (i) $OB=OC$ and both triangles share a common side $AO$. We use side-side-side congruence of triangles and have
\[\Delta ABO\cong \Delta ACO\]
So their corresponding angles to equal sides will be equal. So we have the opposite angles of equal common sides $OB=OC$ as $\angle BAO=\angle CAO$ which means $\overline{AO}$ is the bisector of $\angle A$. Hence it is proved. \[\]

Note: We should not try to find congruence with sides $AO=AO, OB=OC$ and angles $\angle ABO=\angle ACO$ because side-side-angle does not give us congruence condition. It gives a similarity condition which implies the sides opposite to equal angles will be in proportion. We can infer from the proof that angle bisectors of a triangle coincide and the point of coincidence is called in-center which in our figure is O where we can draw the in-circle.