Question

In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitude.

Answer 1

Hint: Here, we will first assume that the length of the sides of the equilateral triangle is equal to ‘a’ units. Then, we will drop an altitude from a vertex to one of its sides and find its length to prove the given statement.

Complete Step-by-Step solution:
Consider a triangle ABC which is equilateral.
              

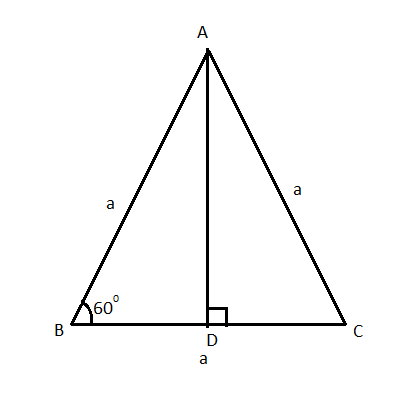
Let us assume that the length of each side of the equilateral triangle is ‘a’ units.
Drop a perpendicular AD from the A on the side BC of the triangle.
Since AD is perpendicular to BC, we can say that $\angle ADB={{90}^{0}}$.
Also, as ABC is an equilateral triangle, so all the sides are of equal length and all the angles are equal to 60 degrees.
Therefore, AB = a units and $\angle ABC={{60}^{0}}$.
Now, according to the angle sum property of the triangle, the sum of all the angles of a triangle is equal to 180 degrees.
So, in triangle ABD, we can write:
$\begin{align}
  & \angle ABD+\angle ADB+\angle BAD={{180}^{0}} \\
 & \Rightarrow {{60}^{0}}+{{90}^{0}}+\angle BAD={{180}^{0}} \\
 & \Rightarrow {{150}^{0}}+\angle BAD={{180}^{0}} \\
 & \Rightarrow \angle BAD={{180}^{0}}-{{150}^{0}}={{30}^{0}} \\
\end{align}$
We know that for any angle $\theta $ , we have:
$\cos \theta =\dfrac{\text{length of base}}{\text{length of hypotenuse}}$
So, in triangle ABD, we can write:
\[\begin{align}
  & \cos \left( \angle BAD \right)=\dfrac{AD}{AB} \\
 & \Rightarrow \cos {{30}^{0}}=\dfrac{AD}{AB} \\
 & \Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{AD}{a} \\
 & \Rightarrow \sqrt{3}a=2\times AD \\
\end{align}\]
On, squaring both sides, we get:
$\begin{align}
  & {{\left( \sqrt{3}a \right)}^{2}}={{\left( 2\times AD \right)}^{2}} \\
 & \Rightarrow 3\times {{a}^{2}}=4\times A{{D}^{2}} \\
 & \\
\end{align}$
Here, we can see that a is the length of one of the sides of the equilateral triangle and AD is the length of the altitude. So, we can write as:
$3\times {{\left( \text{length of one side} \right)}^{2}}=4\times {{\left( \text{length of altitude} \right)}^{2}}$
Hence, we have proved that three times the square of one side in an equilateral triangle is equal to four times the square of one of its altitudes.

Note: Students should note here that in an equilateral triangle, the measure of each of the angles is 60 degrees. Students should also know about the angle sum property of a triangle in order to find the value of an unknown angle. Here, one can also use other trigonometric ratios instead of cosine to arrive at the required conclusion.