Question

In an equilateral \[\Delta ABC\], D is a point on side BC such that 4BD = BC. Prove that, \[16A{{D}^{2}}=13B{{C}^{2}}\].

Answer 1

Hint: In an equilateral triangle all sides are equal. Draw \[AE\bot BC\]. Consider the new triangle formed AED and AEB, find the relation connecting the triangle using Pythagoras theorem. Substitute the necessary values and simplify them.

Complete step-by-step solution -
From the figure, you can see an equilateral triangle ABC.
 

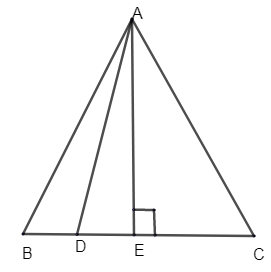
We know that in an equilateral triangle, all the sides are equal. Thus we can say that length AB, BC and AC are the same, which means that,
AB = BC = AC.
It is given that, 4BD = BC, which means that, \[BD=\dfrac{BC}{4}\].
Let us draw AE perpendicular to BC, i.e. \[AE\bot BC\] and point E divides length BC into two equal halves.
i.e. \[BE=EC=\dfrac{BC}{2}\]
Thus we can say that in an equilateral triangle perpendicular drawn from vertex to base bisects the base.
Now let us consider, \[\Delta AED\].
 AE is perpendicular to BC. So, \[\angle AED={{90}^{\circ }}\], which makes \[\Delta AED\] right angled triangles. Thus by Pythagoras theorem we can write that,
\[A{{D}^{2}}=A{{E}^{2}}+D{{E}^{2}}-(1)\]
Now let us consider, \[\Delta AEB\].
\[\angle AEB={{90}^{\circ }}\]
So by Pythagoras theorem, we can write that,
\[A{{B}^{2}}=A{{E}^{2}}+B{{E}^{2}}-(2)\]
From equation (1), \[A{{E}^{2}}=A{{D}^{2}}-D{{E}^{2}}\].
From equation (2), \[A{{E}^{2}}=A{{B}^{2}}-B{{E}^{2}}\].
Now let us equate both the equations.
\[\begin{align}
  & A{{D}^{2}}-D{{E}^{2}}=A{{B}^{2}}-B{{E}^{2}} \\
 & A{{D}^{2}}=A{{B}^{2}}-B{{E}^{2}}+D{{E}^{2}}-(3) \\
\end{align}\]
We said that, \[BE=\dfrac{BC}{2}\] and AB = BC {as it is an equilateral triangle}.
From figure, DE = BE – BD.
Thus substitute these values in equation (3).
\[\therefore A{{D}^{2}}=B{{C}^{2}}-{{\left( \dfrac{BC}{2} \right)}^{2}}+{{\left( BE-BD \right)}^{2}}\]
We know that, \[BE=\dfrac{BC}{2}\]and \[BD=\dfrac{BC}{4}\].
\[\begin{align}
  & \therefore A{{D}^{2}}=B{{C}^{2}}-{{\left( \dfrac{BC}{2} \right)}^{2}}+{{\left( \dfrac{BC}{2}-\dfrac{BC}{4} \right)}^{2}} \\
 & A{{D}^{2}}=B{{C}^{2}}-\dfrac{B{{C}^{2}}}{4}+B{{C}^{2}}{{\left[ \dfrac{1}{2}-\dfrac{1}{4} \right]}^{2}} \\
\end{align}\]
\[A{{D}^{2}}=B{{C}^{2}}\left[ 1-\dfrac{1}{4}+{{\left( \dfrac{2-1}{4} \right)}^{2}} \right]\]
\[\begin{align}
  & A{{D}^{2}}=B{{C}^{2}}\left[ 1-\dfrac{1}{4}+\dfrac{1}{16} \right]=B{{C}^{2}}\left[ \dfrac{16-4+1}{16} \right] \\
 & A{{D}^{2}}=B{{C}^{2}}\left[ \dfrac{13}{16} \right] \\
 & \Rightarrow 16A{{D}^{2}}=13B{{C}^{2}} \\
\end{align}\]
Thus we proved that, \[16A{{D}^{2}}=13B{{C}^{2}}\].

Note: In order to prove, \[16A{{D}^{2}}=13B{{C}^{2}}\], you should substitute all values in terms of BC only. If you substitute any other term, we won’t be able to make the relation connecting AD and BC. Thus make sure to convert all lengths in terms of BC.