
In an ammeter 0.2% of main current passes through the galvanometer. If the resistance galvanometer is G, the resistance of the ammeter will be.
Answer
606.3k+ views
Hint: In this question first we draw an ammeter by connecting a resistance ${R_{sh}}$ in a shunt across the galvanometer whose resistance is given as $G\Omega $. Then equating the potential as they are connected in parallel that is ${V_{Rsh}} = {V_G}$ we get the value of shunt resistance as ${R_{sh}} = \dfrac{2}{{998}} \times G$. Then we solve for total ammeter resistance that is ${R_A} = {R_{sh}}\parallel G$ and get the required answer.
Complete Step-by-Step solution:
The first step is to know how an ammeter is constructed using a galvanometer. When we connect a parallel resistance across the galvanometer with very low resistance. And as mentioned in the question that only 0.2% of the main current is passing through the galvanometer. So we have drawn the ammeter with all the current components as shown in figure 1.
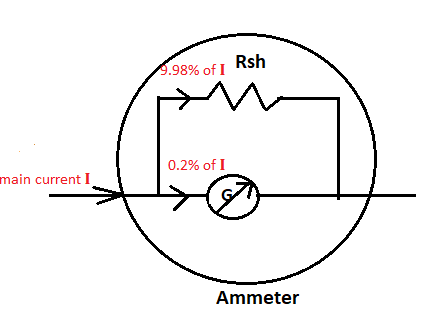
Here, let us assume the main current be \[I\]
So current through galvanometer is ${I_G} = 0.2\% I = \dfrac{2}{{1000}}I$
Now the current through the shunt resistance ${R_{sh}}$ is
${I_{sh}} = I - {I_G} = I - \dfrac{2}{{1000}}I$
$ \Rightarrow {I_{sh}} = \dfrac{{998}}{{1000}}I$
Now we are given that the resistance of the galvanometer is $G\Omega $, So to find the overall resistance of ammeter ${R_A}$ that is the parallel combination of ${R_{sh}}$ and $G\Omega $, we need to calculate ${R_{sh}}$.
${R_A} = {R_{sh}}\parallel G$
From the figure we can see that the potential across ${R_{sh}}$ is same as potential across $G$ that is
${V_{Rsh}} = {V_G}$
$ \Rightarrow {I_{sh}} \times {R_{sh}} = {I_G} \times G$
$ \Rightarrow \dfrac{{998}}{{1000}}{I} \times {R_{sh}} = \dfrac{2}{{1000}}{I} \times G$
$ \Rightarrow {R_{sh}} = \dfrac{2}{{998}} \times G$
Now ${R_A} = {R_{sh}}\parallel G$
\[ \Rightarrow {R_A} = \dfrac{2}{{998}}G\parallel G\]
$ \Rightarrow {R_A} = \dfrac{1}{{499}}G\parallel G$
Now by solving this we will get
$ \Rightarrow {R_A} = \dfrac{{\dfrac{1}{{499}}G \times G}}{{\dfrac{1}{{499}}G + G}} = \dfrac{{{{{G}}^2}}}{{{G}\left( {499 + 1} \right)}}$
$ \Rightarrow {R_A} = \dfrac{G}{{500}}\Omega $
Therefore the overall ammeter resistance is $\dfrac{G}{{500}}\Omega $
Note: For these kinds of questions we first need to know how to construct an ammeter, voltmeter, and wattmeter using a galvanometer. Then we can find the overall resistances either by parallel connection or by the series connection of all the resistance that is present. We also need to have a good knowledge of KVL and KCL.
Complete Step-by-Step solution:
The first step is to know how an ammeter is constructed using a galvanometer. When we connect a parallel resistance across the galvanometer with very low resistance. And as mentioned in the question that only 0.2% of the main current is passing through the galvanometer. So we have drawn the ammeter with all the current components as shown in figure 1.

Figure1
Here, let us assume the main current be \[I\]
So current through galvanometer is ${I_G} = 0.2\% I = \dfrac{2}{{1000}}I$
Now the current through the shunt resistance ${R_{sh}}$ is
${I_{sh}} = I - {I_G} = I - \dfrac{2}{{1000}}I$
$ \Rightarrow {I_{sh}} = \dfrac{{998}}{{1000}}I$
Now we are given that the resistance of the galvanometer is $G\Omega $, So to find the overall resistance of ammeter ${R_A}$ that is the parallel combination of ${R_{sh}}$ and $G\Omega $, we need to calculate ${R_{sh}}$.
${R_A} = {R_{sh}}\parallel G$
From the figure we can see that the potential across ${R_{sh}}$ is same as potential across $G$ that is
${V_{Rsh}} = {V_G}$
$ \Rightarrow {I_{sh}} \times {R_{sh}} = {I_G} \times G$
$ \Rightarrow \dfrac{{998}}{{1000}}{I} \times {R_{sh}} = \dfrac{2}{{1000}}{I} \times G$
$ \Rightarrow {R_{sh}} = \dfrac{2}{{998}} \times G$
Now ${R_A} = {R_{sh}}\parallel G$
\[ \Rightarrow {R_A} = \dfrac{2}{{998}}G\parallel G\]
$ \Rightarrow {R_A} = \dfrac{1}{{499}}G\parallel G$
Now by solving this we will get
$ \Rightarrow {R_A} = \dfrac{{\dfrac{1}{{499}}G \times G}}{{\dfrac{1}{{499}}G + G}} = \dfrac{{{{{G}}^2}}}{{{G}\left( {499 + 1} \right)}}$
$ \Rightarrow {R_A} = \dfrac{G}{{500}}\Omega $
Therefore the overall ammeter resistance is $\dfrac{G}{{500}}\Omega $
Note: For these kinds of questions we first need to know how to construct an ammeter, voltmeter, and wattmeter using a galvanometer. Then we can find the overall resistances either by parallel connection or by the series connection of all the resistance that is present. We also need to have a good knowledge of KVL and KCL.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




