
In an action film, hero is supposed to throw a grenade from his car, which is going at $ 90km{{h}^{-1}} $ , to his enemy’s car, which is going at $ 110km{{h}^{-1}} $ . The enemy’s car is $ 15.8m $ in front of the hero’s car when he lets go of the grenade. If the hero throws the grenade such that its initial velocity is at an angle of $ 45{}^\circ $ above the horizontal, what should the magnitude of the initial velocity be? Both the cars are traveling in the same direction on a levelled road. Ignore air resistance. Find the magnitude of the velocity relative to the earth (in $ m{{s}^{-1}} $ )
(A) $ 38 $
(B) $ 39 $
(C) $ 40 $
(D) $ 41 $
Answer
516k+ views
Hint: To find the velocity of the grenade relative to earth, we can initially find its velocity relative to the hero’s car. For the grenade to hit the enemy’s car the $ x $ - coordinate of the grenade should be equal to that of the enemy's car, while the $ y $ - coordinate should be equal to zero.
Complete step by step solution:
To begin, let us note down the given data;
Velocity of hero’s car $ {{v}_{h}}=90km{{h}^{-1}} $
We need to convert the velocity in SI units
$ {{v}_{h}}=90\times \dfrac{1000m}{3600s} $
$ {{v}_{h}}=90\times \dfrac{5m}{18s} $
From here, we can understand that the conversion factor to convert $ km{{h}^{-1}} $ to $ m{{s}^{-1}} $ is $ \dfrac{5}{18} $
Without considering the units,
$ {{v}_{h}}=90\times \dfrac{5}{18} $
$ {{v}_{h}}=25m{{s}^{-1}} $
Velocity of enemy’s car $ {{v}_{e}}=110km{{h}^{-1}} $
To convert to SI units, we will multiply by the conversion factor,
$ {{v}_{e}}=110\times \dfrac{5}{18} $
$ {{v}_{e}}=30.5m{{s}^{-1}} $
Distance between the hero’s car and the enemy’s car $ d=15.8m $
Velocity of the grenade with respect to hero’s car $ {{v}_{g}}=? $
Angle of velocity of grenade with respect to horizontal $ \theta =45{}^\circ $
As the velocity is inclined, we can divide it in its horizontal and vertical components.
The situation can be explained as shown in the figure below;
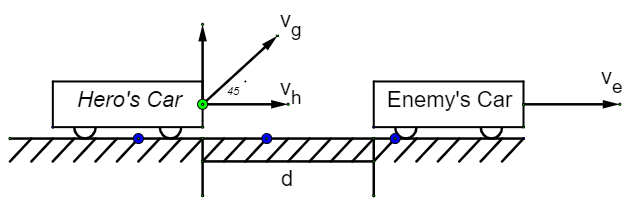
We will consider the hero’s car to be the reference point.
Now, the distance travelled by the grenade in horizontal direction in terms of time is given as,
$ x(t)=\left( {{v}_{g}}\cos 45{}^\circ \right)t $ …… $ (1) $
And, the distance travelled in the vertical direction is given from the equation of uniformly accelerated motion,
$ y(t)=ut+\dfrac{1}{2}a{{t}^{2}} $
$ y(t)=\left( {{v}_{g}}\sin 45{}^\circ \right)t+\dfrac{1}{2}(-g){{t}^{2}} $
Here, negative sign shows that the motion is opposite to the gravity,
$ y(t)=\left( {{v}_{g}}\sin 45{}^\circ \right)t-\dfrac{1}{2}g{{t}^{2}} $ …… $ (2) $
$ y(t)=\left[ \left( {{v}_{g}}\sin 45{}^\circ \right)-\dfrac{1}{2}gt \right]t $
Dividing the whole equation by time.
$ \dfrac{y(t)}{t}=\left[ \left( {{v}_{g}}\sin 45{}^\circ \right)-\dfrac{1}{2}gt \right] $
$ {{v}_{y}}(t)=\left( {{v}_{g}}\sin 45{}^\circ \right)-\dfrac{1}{2}gt $ …… $ (3) $
Now, the distance travelled by the enemy’s car with respect to hero’s car in terms of time including the distance between the cars is
$ x(t)=d+({{v}_{e}}-{{v}_{h}})t $
Substituting the given values,
$ x(t)=15.8+(30.5-25)t $
$ x(t)=15.8+5.5t $ …… $ (4) $
Now, we know that for the grenade to hit the enemy’s car, its distance in $ y $ direction should be zero.
From equation $ (2) $ ,
$ 0=\left( {{v}_{g}}\sin 45{}^\circ \right)t-\dfrac{1}{2}g{{t}^{2}} $
$ 0=\left( {{v}_{g}}\sin 45{}^\circ \right)-\dfrac{1}{2}gt $
Substituting the predefined values,
$ 0=\left( \dfrac{{{v}_{g}}}{\sqrt{2}} \right)-\dfrac{1}{2}(9.8)t $
$ \dfrac{1}{2}(9.8)t=\left( \dfrac{{{v}_{g}}}{\sqrt{2}} \right) $
For finding the time in terms of velocity of grenade,
$ t=\dfrac{{{v}_{g}}}{\sqrt{2}}\times \dfrac{2}{9.8} $
$ t=0.144{{v}_{g}} $ …… $ (5) $
Also, for the grenade to hit the enemy’s car, the distance covered in $ x $ direction should be equal.
Equating the equations $ (1) $ and $ (4) $ ,
$ \left( {{v}_{g}}\cos 45{}^\circ \right)t=15.8+5.5t $
Substituting the value obtained in equation $ (5) $ ,
$ \left( {{v}_{g}}\cos 45{}^\circ \right)\left( 0.144{{v}_{g}} \right)=15.8+5.5\left( 0.144{{v}_{g}} \right) $
$ \dfrac{{{v}_{g}}^{2}}{10}=15.8+0.792{{v}_{g}} $
Rearranging the equation to get a quadratic form,
$ {{v}_{g}}^{2}-7.92{{v}_{g}}-158=0 $
Solving the quadratic equation,
$ {{v}_{g}}=\dfrac{7.92\pm \sqrt{{{(7.92)}^{2}}-4(1)(-158)}}{2(1)} $
$ {{v}_{g}}\approx 17m{{s}^{-1}} $
This is the velocity of the grenade with respect to the hero’s car.
The velocity of the grenade with respect to the earth is calculated as,
$ v=\sqrt{{{\left( {{v}_{g}}\cos 45{}^\circ +{{v}_{h}} \right)}^{2}}+{{\left( {{v}_{g}}\sin 45{}^\circ \right)}^{2}}} $ , because we need to include the velocity of hero’s car from which the grenade was released in the horizontal component.
Substituting the obtained values,
$ v=\sqrt{{{\left( 17\times \dfrac{1}{\sqrt{2}}+25 \right)}^{2}}+{{\left( 17\times \dfrac{1}{\sqrt{2}} \right)}^{2}}} $
$ v=39m{{s}^{-1}} $
Hence, the correct answer is Option $ (B) $.
Note:
Here, as the grenade was released at an angle with the horizontal, we can also use the equations of the projectile motion, where by substituting the equation of range as the distance traveled and equation of time taken in the equation $ (4) $, we can directly obtain the value of velocity of grenade with respect to hero’s car.
Complete step by step solution:
To begin, let us note down the given data;
Velocity of hero’s car $ {{v}_{h}}=90km{{h}^{-1}} $
We need to convert the velocity in SI units
$ {{v}_{h}}=90\times \dfrac{1000m}{3600s} $
$ {{v}_{h}}=90\times \dfrac{5m}{18s} $
From here, we can understand that the conversion factor to convert $ km{{h}^{-1}} $ to $ m{{s}^{-1}} $ is $ \dfrac{5}{18} $
Without considering the units,
$ {{v}_{h}}=90\times \dfrac{5}{18} $
$ {{v}_{h}}=25m{{s}^{-1}} $
Velocity of enemy’s car $ {{v}_{e}}=110km{{h}^{-1}} $
To convert to SI units, we will multiply by the conversion factor,
$ {{v}_{e}}=110\times \dfrac{5}{18} $
$ {{v}_{e}}=30.5m{{s}^{-1}} $
Distance between the hero’s car and the enemy’s car $ d=15.8m $
Velocity of the grenade with respect to hero’s car $ {{v}_{g}}=? $
Angle of velocity of grenade with respect to horizontal $ \theta =45{}^\circ $
As the velocity is inclined, we can divide it in its horizontal and vertical components.
The situation can be explained as shown in the figure below;

We will consider the hero’s car to be the reference point.
Now, the distance travelled by the grenade in horizontal direction in terms of time is given as,
$ x(t)=\left( {{v}_{g}}\cos 45{}^\circ \right)t $ …… $ (1) $
And, the distance travelled in the vertical direction is given from the equation of uniformly accelerated motion,
$ y(t)=ut+\dfrac{1}{2}a{{t}^{2}} $
$ y(t)=\left( {{v}_{g}}\sin 45{}^\circ \right)t+\dfrac{1}{2}(-g){{t}^{2}} $
Here, negative sign shows that the motion is opposite to the gravity,
$ y(t)=\left( {{v}_{g}}\sin 45{}^\circ \right)t-\dfrac{1}{2}g{{t}^{2}} $ …… $ (2) $
$ y(t)=\left[ \left( {{v}_{g}}\sin 45{}^\circ \right)-\dfrac{1}{2}gt \right]t $
Dividing the whole equation by time.
$ \dfrac{y(t)}{t}=\left[ \left( {{v}_{g}}\sin 45{}^\circ \right)-\dfrac{1}{2}gt \right] $
$ {{v}_{y}}(t)=\left( {{v}_{g}}\sin 45{}^\circ \right)-\dfrac{1}{2}gt $ …… $ (3) $
Now, the distance travelled by the enemy’s car with respect to hero’s car in terms of time including the distance between the cars is
$ x(t)=d+({{v}_{e}}-{{v}_{h}})t $
Substituting the given values,
$ x(t)=15.8+(30.5-25)t $
$ x(t)=15.8+5.5t $ …… $ (4) $
Now, we know that for the grenade to hit the enemy’s car, its distance in $ y $ direction should be zero.
From equation $ (2) $ ,
$ 0=\left( {{v}_{g}}\sin 45{}^\circ \right)t-\dfrac{1}{2}g{{t}^{2}} $
$ 0=\left( {{v}_{g}}\sin 45{}^\circ \right)-\dfrac{1}{2}gt $
Substituting the predefined values,
$ 0=\left( \dfrac{{{v}_{g}}}{\sqrt{2}} \right)-\dfrac{1}{2}(9.8)t $
$ \dfrac{1}{2}(9.8)t=\left( \dfrac{{{v}_{g}}}{\sqrt{2}} \right) $
For finding the time in terms of velocity of grenade,
$ t=\dfrac{{{v}_{g}}}{\sqrt{2}}\times \dfrac{2}{9.8} $
$ t=0.144{{v}_{g}} $ …… $ (5) $
Also, for the grenade to hit the enemy’s car, the distance covered in $ x $ direction should be equal.
Equating the equations $ (1) $ and $ (4) $ ,
$ \left( {{v}_{g}}\cos 45{}^\circ \right)t=15.8+5.5t $
Substituting the value obtained in equation $ (5) $ ,
$ \left( {{v}_{g}}\cos 45{}^\circ \right)\left( 0.144{{v}_{g}} \right)=15.8+5.5\left( 0.144{{v}_{g}} \right) $
$ \dfrac{{{v}_{g}}^{2}}{10}=15.8+0.792{{v}_{g}} $
Rearranging the equation to get a quadratic form,
$ {{v}_{g}}^{2}-7.92{{v}_{g}}-158=0 $
Solving the quadratic equation,
$ {{v}_{g}}=\dfrac{7.92\pm \sqrt{{{(7.92)}^{2}}-4(1)(-158)}}{2(1)} $
$ {{v}_{g}}\approx 17m{{s}^{-1}} $
This is the velocity of the grenade with respect to the hero’s car.
The velocity of the grenade with respect to the earth is calculated as,
$ v=\sqrt{{{\left( {{v}_{g}}\cos 45{}^\circ +{{v}_{h}} \right)}^{2}}+{{\left( {{v}_{g}}\sin 45{}^\circ \right)}^{2}}} $ , because we need to include the velocity of hero’s car from which the grenade was released in the horizontal component.
Substituting the obtained values,
$ v=\sqrt{{{\left( 17\times \dfrac{1}{\sqrt{2}}+25 \right)}^{2}}+{{\left( 17\times \dfrac{1}{\sqrt{2}} \right)}^{2}}} $
$ v=39m{{s}^{-1}} $
Hence, the correct answer is Option $ (B) $.
Note:
Here, as the grenade was released at an angle with the horizontal, we can also use the equations of the projectile motion, where by substituting the equation of range as the distance traveled and equation of time taken in the equation $ (4) $, we can directly obtain the value of velocity of grenade with respect to hero’s car.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




