Question

In adjoining trapezium\[ABCD\],\[AB = 6,DC = 12,CF = 9,AO = 4,BC = 10\],

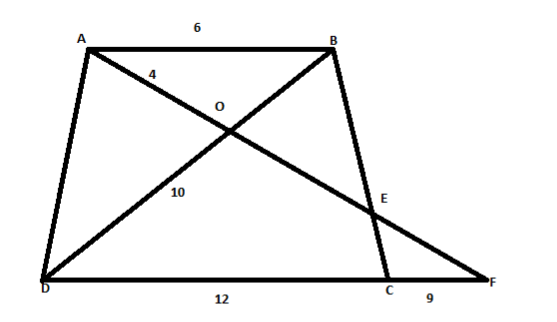
Calculate
i) \[EC\]
ii) \[EF\]
iii) \[OE\]

Answer 1

Hint: At first, we will construct the trapezium\[ABCD\] and add a point\[F\]outside the trapezium which is at\[9\]steps from\[C\], we will use the triangles that are formed by the line \[BD\& AF\]and try to find the similarity of the triangles. From there we will find the values of the required sides.

Complete step by step solution:
The given figure is,

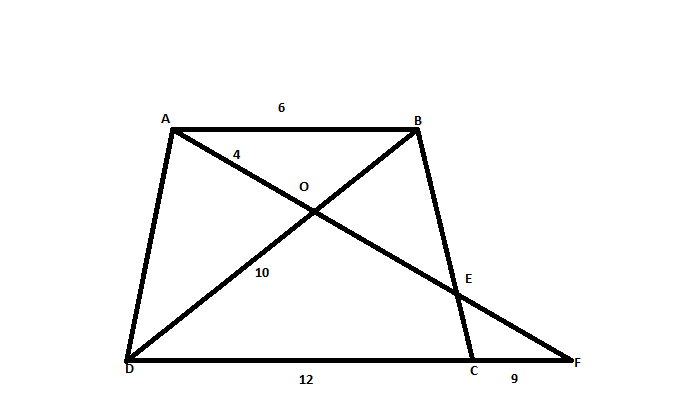
It is given that in the trapezium\[ABCD\], \[AB = 6,DC = 12,CF = 9,AO = 4,BC = 10\]
Since, \[AB\parallel CD, AF\] is the transversal by the definition of a trapezium so, the alternate interior angles of the trapezium are equal.
So, \[\angle CFE = \angle EAB\]
Again, \[\angle CEF = \angle AEB\] as they are vertically opposite angles formed in the given trapezium.
So, in trapezium \[ABCD\]\[\Delta CFE\& \Delta EAB\] are similar triangle.
Therefore, we get, \[\dfrac{{EC}}{{EB}} = \dfrac{{CF}}{{AB}}\]by the property of triangles.
Here\[EB = BC - EC\]
And we have other values too. Let us substitute the values, then we get,
\[\dfrac{{EC}}{{BC - EC}} = \dfrac{9}{6}\]
Let us simplify and substitute the value we know, so that we get,
\[\dfrac{{EC}}{{10 - EC}} = \dfrac{3}{2}\]
Again by cross multiplication we get,
\[2EC = 30 - 3EC\]
Finally, on simplification we get,
\[EC = 6\]
Similarly consider\[\Delta ODF\& \Delta OAB\],
\[\angle OFD = \angle BAO\] as they are alternate interior angles.
\[\angle DOF = \angle AOB\]as they are vertically opposite angles.
So, in the given trapezium \[\Delta ODF\& \Delta OAB\]are similar triangles.
\[\dfrac{{OF}}{{AO}} = \dfrac{{DE}}{{AB}}\]by property of triangles.
Here\[DE = DC + CF\], on substituting the known values in the above equation we get,
\[\dfrac{{OF}}{4} = \dfrac{{DC + CF}}{6}\]
Let us substitute the values then we get,
\[\dfrac{{OF}}{4} = \dfrac{{12 + 9}}{6} = \dfrac{7}{2}\]
On cross multiplying and solving we get,
\[OF = 14\]
Similarly \[\Delta CFE\& \Delta EAB\]are similar triangle.
\[\dfrac{{EF}}{{AE}} = \dfrac{{CF}}{{AB}}\]
Here\[AE = AF - EF\] , let us substitute the known values in the above equation we get,
\[\dfrac{{EF}}{{AF - EF}} = \dfrac{9}{6}\]
On further substitution of known values we get,
\[\dfrac{{EF}}{{18 - EF}} = \dfrac{3}{2}\]
On cross multiplying and solving we get,
\[EF = 10.8\]
Therefore,
\[OE = OF - EF = 14 - 10.8 = 3.2cm\]

$\therefore$The required values are \[EC = 6cm,OE = 3.2cm,EF = 10.8cm\].

Additional Information:
Two triangles are said to be similar if one angle of a triangle is equal to one angle of another triangle and the sides including these angles are proportional or two angles of a triangle are equal two angles of another triangle or three sides of one triangle are proportional to the three sides of another triangle.

Note:
We should be careful in finding similar triangles because the finding of a similar triangles plays a major role in the given problem suppose we choose different triangles there could arise the problem of similarity.