Question

In a village one half of the population works in the fields. Half of the people who do not work in the fields are working in factories. Select the appropriate diagram in which shaded region is best representing people working in the factories.
(a)

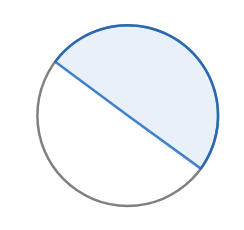
(b)

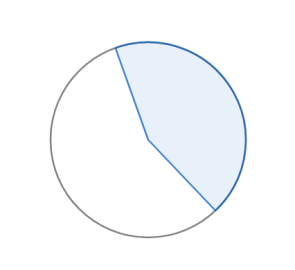
(c)

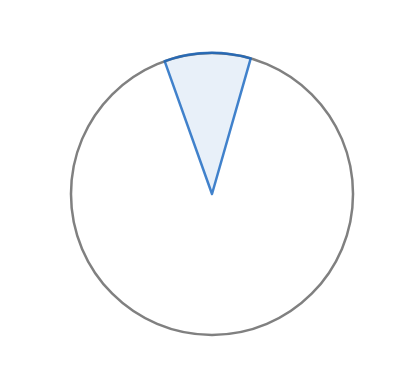
(d)

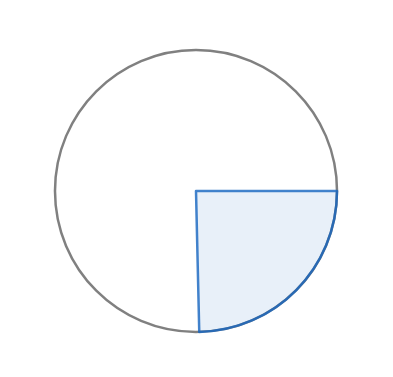
Answer 1

Hint: Convert the data given in the question into fractions. Convert the pie diagrams in the options into corresponding fractions. Compare both to obtain the answer. Parts of a whole are represented as fractions and percentages.

Complete step by step answer:
We are given that one half of the population works in the fields or in other words $\dfrac{1}{2}$ of the population works in the fields. We are also given that half of the people who do not work in the fields are working in the factories.
In other words $\dfrac{1}{2}$ of the people who do not work in the fields works in the factory.
The above mentioned fraction of people who works in factory can further be written as,
 $\dfrac{1}{2}$ of ($\dfrac{1}{2}$ of the population).
 $\dfrac{1}{2} \times (\dfrac{1}{2}$ of the population)=$\dfrac{1}{4}$ of the population
Hence, $\dfrac{1}{4}$ of the population works in the factory.
Now we need to convert the pie diagrams into equivalent fractions, that is, how much of the circle’s (or pie’s) area is shaded.
We can easily find option (d) corresponds to quarter of total area of the circle(or pie)
Option (d) best depicts this fraction.

So, the correct answer is “Option D”.

Note: This question can also be done in terms of percentages. Fractions are parts of a whole. 100% represents a whole (or simply 1).
$\dfrac{1}{2}$ of the population means half of the 100% population, which of course is 50% of the population.
Likewise, $\dfrac{1}{2}$ of ($\dfrac{1}{2}$ of the population) is nothing but 50% of 50% of the population, which is further 25% of the population, $\dfrac{1}{4}$ of the population.