Question

In a uniform electric field, the equipotential surfaces must be:
This question has multiple correct options
a) be plane surfaces
b) be normal to the direction of the field
c) be placed such that the surfaces having equal differences in potential are separated by equal differences
d) have decreasing potential in the direction of the field

Answer 1

Hint: The question is of the type multiple correct options. Hence, eliminate the wrong options using the properties of equipotential surfaces in an electric field. The understanding of the relation between Electric field and potential is essential to choose the right options.

Complete solution:
Let us first define the equipotential potential surfaces, understand the properties and the relation between electric field and electrostatic potential which results in equipotential surfaces.
An equipotential surface is a surface with a constant value of potential at all the points on the surface.
Since, to move a charge q from a region of one potential let us say A to some other potential let us say B work done is give by $\dfrac{W}{q}={{V}_{B}}-{{V}_{A}}J$
Now since we know that on an equipotential surface, potential is the same, work done to move a charge between any two points i.e.

$\dfrac{W}{q}={{V}_{B}}-{{V}_{A}}J$
$\begin{align}
  & \dfrac{W}{q}=V-V \\
 & W=0J \\
\end{align}$

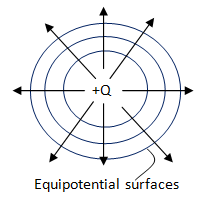
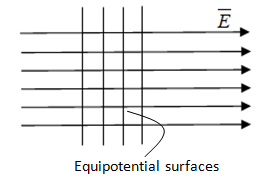
As shown in the above diagram 1 the concentric circles about a charge +Q are the equipotential surfaces. Similarly the normal lines drawn to uniform electric fields also represent equipotential surfaces.
If we observe the above diagram the equipotential surfaces are always normal to the electric field. This is because if the electric field was not perpendicular to the equipotential surface there would have existed some non zero component of along the surface . Hence to move a test charge along the direction of the field work had to be done. But this contradicts the definition of an equipotential surface. Hence the electric field is always perpendicular to the surface.
Let us obtain the relation between electric field and potential.
Work done to move a charge between two points in an electric field is given by,
$\dfrac{W}{q}={{V}_{B}}-{{V}_{A}}J..........(1)$
But by general definition of work done , work done is given as
$W=\overline{F}\times d.......(2)$
Here $\overline{F}$is the electrostatic force and d is the distance through which the charge is moved.
Let us assume that the charge is ,moved through a small distance $dr$ trough a region of potential $dV$
Equating equation 1 and 2 for work done we get,
$({{V}_{B}}-{{V}_{A}})q=-\overline{F}.d$ the minus sign suggests the force and displacement are in opposite directions.
 Since we assumed that the charge is ,moved through a small distance $dr$ trough a region of potential $dV$.
The above equation becomes
$dVq=-\overline{F}.dr$
Electrostatic force on a charge is given by, F=Eq, where E is the electric field and q is the charge on which force is acted upon. Hence,

$\begin{align}
  & dVq=-\overline{F}.dr \\
 & dVq=-\overline{E}qdr \\
\end{align}$

q gets cancelled on both the sides and we get,

$\begin{align}
  & dV=\overline{-E}dr \\
 & \dfrac{dV}{dr}=-\overline{E} \\
\end{align}$

The minus sign suggested with the electric field is in the direction of decreasing potential .
Hence from all the above results obtained Its not necessary for the equipotential surfaces to be plane surfaces.
Hence the answer to the above question are option b, c and d.
b) be normal to the direction of the field
c) be placed such that the surfaces having equal differences in potential are separated by equal differences since $\dfrac{dV}{dr}=-\overline{E}$ i.e. E is constant and therefore for every change in dV the corresponding dr should be same
d) have decreasing potential in the direction of the field

Note: For a charge q the field is not uniform $\dfrac{dV}{dr}=-\overline{E}$ is not constant for consecutive equipotential surfaces as we move from the centre of the charge but for a uniform field i.e., by a charged plate $\dfrac{dV}{dr}=-\overline{E}$is constant.