Question

In a triangle, the perpendicular from the vertex to the base bisects the base. The triangle is
(a) Isosceles
(b) Right angled
(c) Equilateral
(d) Scalene

Answer 1

Hint: First of all, we need to construct a perpendicular AD to the base BC from vertex A, such that BD = CD. Now, we can prove that two triangles ABD and ACD are congruent to each other. Then, by using CPCT, we can show that AB = AC. We can accordingly select the correct answer.

Complete step by step answer:
Let us assume a triangle ABC, and AD is the perpendicular on base BC, such that BD = CD. Now, we need to find that ABC is which type of triangle. We have shown the figure below,

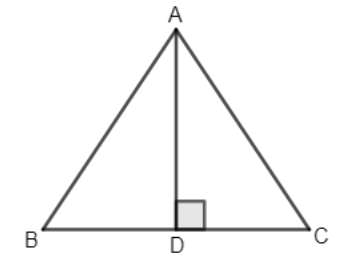
Let us now shift our focus on triangle ABD and triangle ACD.
In these two triangles, we know that BD = CD, since it was already given in the question.
We must note that AD is perpendicular on BC. Thus $\angle ADB=\angle ADC={{90}^{\circ }}$ .
Also, we have the side AD common in both these triangles.
Thus, in triangle ABD and triangle ACD, we have
BD = CD (given)
$\angle ADB=\angle ADC$ (both are right angles)
AD = AD (common)
Thus, by side-angle-side (SAS) criteria, $\Delta ABD\cong \Delta ACD$ .
Now, by corresponding parts of congruent triangles (CPCT),
AB = AC.
We know that if any two sides of a triangle are equal, then the triangle is called an isosceles triangle.
So, now we can clearly call ABC as an isosceles triangle.
From our options, we can see that option (a) is a correct option.
Option (b) is a right angled triangle. Here, we have no conditions through which we can decide the magnitude of any on the angles of triangle ABC. So, this may be true in some cases, but not always. Hence, option (b) is not a correct option.
Option (c) is an equilateral triangle. Here, we have the relation AB = AC, but we don’t have any information regarding the side BC. So, this triangle could be equilateral in some cases, but not always. Hence, option (c) is not a correct option.
Option (d) is scalene triangle. This option is definitely wrong as two of the sides of the triangle are equal. Hence, option (d) is also wrong.

So, the correct answer is “Option a”.

Note: We must take care while mentioning the corresponding parts in CPCT. We must also note that an option that might be correct in a few cases, can never be the answer. This is because we know that an equilateral triangle is always isosceles, and a right angled triangle may also be isosceles.