Question

In a triangle $\Delta ABC$, if O, H and G represents circum-centre, orthocenter and centroid respectively then $GO:HG = $
A) $1:2$
B) $2:1$
C) $1:3$
D) $2:3$

Answer 1

Hint: First make some construction regarding the altitude on BC and median of BC and then use them to show the similarity in the triangles that are needed to show the desired result.

Complete step-by-step solution:
It is given in the problem that O, H, and G represents circum-center, orthocenter, and centroid respectively.
The goal of the problem is to find the ratio $GO: HG$.
First draw a figure that defines a triangle and the points O, H, and G defining circum-center, orthocenter, and centroid respectively. Then the figure is given as:

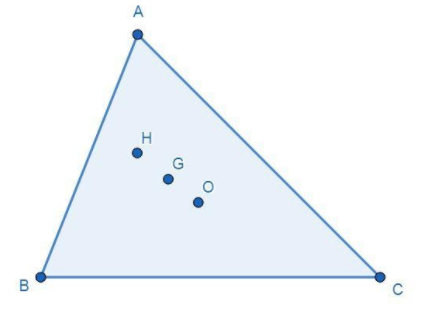
Now, draw an altitude from the vertex A that cuts the side \[BC\] at point P, as $H$ is an orthocenter so AP passes through the point H and assume that Q is the median of the side \[BC\] such that $BQ = QC$. Then construct a line$AQ$. Also draw a line $OQ$, which is perpendicular on the side BC as O is the circum-center. After the construction, the figure is given as:

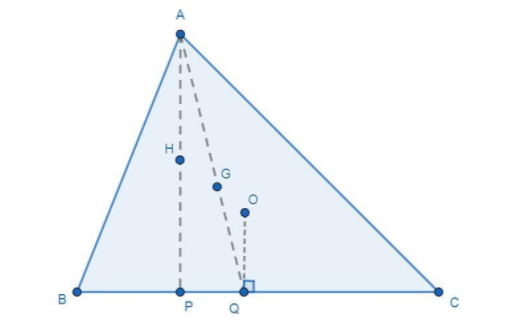
The line $AP||OQ$ as both are perpendicular to the side $BC$ and $AQ$is the transversal line that passes through two lines $AP$ and$OQ$. Now, construct two triangles $\Delta AGH$ and $\Delta QGO$. These triangles are given in a figure as:

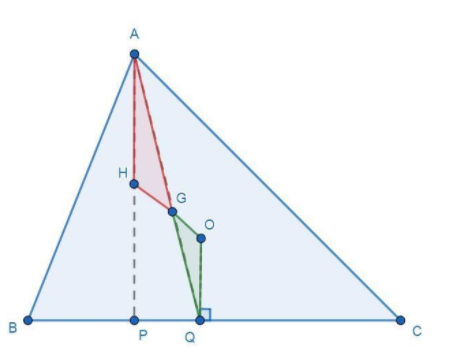
Now, in triangles $\Delta AGH$ and $\Delta QGO$,
$\angle AGH = \angle OGQ$(Vertically opposite angles)
$\angle GAH = \angle GQO$(Alternate angle on A transversal axis)
Then using the \[AAA\] rule of similarity, we have the conclusion that the triangle $\Delta AGH$ and $\Delta QGO$ are similar.
$\Delta AGH \sim \Delta QGO$
Using the property of similarity, the sides of the triangles are in the same proportion. That is,
$\dfrac{{AG}}{{GH}} = \dfrac{{QG}}{{GO}}$
$\dfrac{{AG}}{{QG}} = \dfrac{{GH}}{{GO}}$
As it is given that $G$is the centroid thus it divides the median in $2:1$ ratio. That is,
$AG = 2QG$
SO, the above fraction is given as:
$ \Rightarrow \dfrac{{AG}}{{QG}} = \dfrac{{GH}}{{GO}} = \dfrac{2}{1}$
$\dfrac{{GH}}{{GO}} = \dfrac{2}{1}$
$ \Rightarrow \dfrac{{GO}}{{HG}} = \dfrac{1}{2}$

Hence,the required ratio is: $GO:HG = 1:2$
Therefore, Option (A) is correct.

Note:
There are four similarity tests that make sure that the given triangles are similar.
(1) AAA- If all the three angles of the triangle are the same then the triangles are similar.
(2) ASA- If the ratio of the two sides is equal in both the triangles and the corresponding angles is also same then the triangles are similar.
(3) SSS- If the ratio of all the sides of the triangles is equal then both the triangles are similar.
(4) RHS- If the ratio of the hypotenuse and the one side of the right-angled triangle are the same then the triangles are similar.