Question

In a triangle, $\angle ABC={{150}^{\circ }}$ and P is the orthocenter of triangle ABC. Find the value of $\angle APC$.

Answer 1

Hint: Draw perpendicular lines or altitudes from each vertex A, B and C and assume that they intersect at P, which is the orthocenter of the triangle. Use the property of vertically opposite angles and sum of internal angles of a quadrilateral to find the desired angle.

Complete step-by-step answer:
First of all we need to understand the term ‘orthocenter’. An orthocenter is a point where all the altitudes of a triangle meet each other. It is not necessary that this point lies inside the triangle. This point lies inside the triangle in case of acute angle triangle and lies outside the triangle in case of obtuse angle triangle. In case of a right angle triangle, the orthocenter lies on the vertex that is opposite to the hypotenuse.

Now, we come to the question. Let us draw a rough diagram of the triangle and the angle we need to find. Since the triangle is obtuse at vertex B, its orthocenter lies outside the triangle. Draw perpendicular from vertex A to meet the extended side BC at D. Draw perpendicular from vertex C to meet the extended side AB at E. At last draw perpendicular from vertex B to meet the side AC at F. Extend the line BF backwards so that all the three altitudes meet at point P.

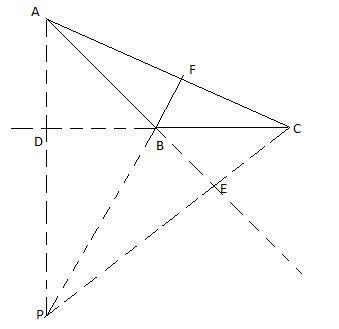
Now, $\angle ABC$ and $\angle DBE$ are vertically opposite angles, therefore they are equal.

$\therefore \angle DBE={{150}^{\circ }}$.

 Now, DBEP is a quadrilateral and we know that the sum of all the internal angles of a quadrilateral is ${{360}^{\circ }}$.

$\begin{align}

  & \therefore \angle BDE+\angle DPE+\angle PEB+\angle DBE={{360}^{\circ }} \\

 & {{90}^{\circ }}+\angle DPE+{{90}^{\circ }}+{{150}^{\circ }}={{360}^{\circ }} \\

 & \angle DPE={{360}^{\circ }}-{{330}^{\circ }} \\

 & \angle DPE={{30}^{\circ }} \\

\end{align}$

Hence, $\angle APC=\angle DPE={{30}^{\circ }}$.

Note: Don’t make the diagram of acute angle triangle because it is given that the triangle is an obtuse angle triangle. Failing to do so can mislead our answer. Also, we have used the concept of vertically opposite angles to determine the third angle of the quadrilateral, so that the fourth angle can be determined.