Question

In a triangle ABC, DE is parallel to BC. If \[\dfrac{{AD}}{{DB}} = \dfrac{2}{3}\] and AC = 18 cm, then find AE.

Answer 1

Hint: Draw triangle ABC and DE parallel to BC. Prove that the two triangles are similar and then use the properties of similar triangles to find the relation between AE and AC and then find AE.

Complete step-by-step answer:

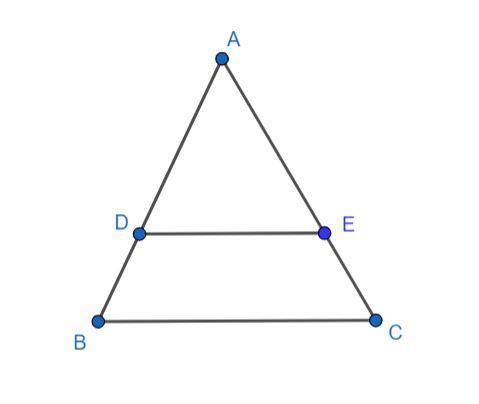
In the diagram, ABC is a triangle and the line segment DE is parallel to BC.
Let us check triangle ABC and triangle ADE for similarity.
We know that corresponding angles on two parallel lines are equal. Hence, angle ADE is equal to angle ABC and angle AED is equal to angle ACB.
\[\angle ADE = \angle ABC..............(1)\]
\[\angle AED = \angle ACB..............(2)\]
Angle A is common between both the triangles. Hence, we have:
\[\angle EAD = \angle BAC..............(3)\]
From equation (1), equation (2) and equation (3), the triangles ABC and ADE are similar by Angle-Angle-Angle (AAA) criterion. Hence, we have:
\[\Delta ABC \sim \Delta ADE\]
We know that the properties of similar triangles states that the ratio of corresponding sides of similar triangles are equal.
For triangle ABC and triangle ADE, we have AB and AD, AC and AE, BC and DE as corresponding sides. Hence, the ratio of AB by AD is equal to the ratio of AC by AE is equal to the ratio of BC by DE.
Hence, we have as follows:
\[\dfrac{{AB}}{{AD}} = \dfrac{{AC}}{{AE}} = \dfrac{{BC}}{{DE}}\]
Now, considering the first two equal terms we have:
\[\dfrac{{AB}}{{AD}} = \dfrac{{AC}}{{AE}}\]
We know that AB = AD + DB, then, we have:
\[\dfrac{{AD + DB}}{{AD}} = \dfrac{{AC}}{{AE}}\]
Simplifying, we have:
\[1 + \dfrac{{DB}}{{AD}} = \dfrac{{AC}}{{AE}}\]
It is given that \[\dfrac{{AD}}{{DB}} = \dfrac{2}{3}\] and AC = 18 cm. Hence, we have:
\[1 + \dfrac{3}{2} = \dfrac{{18}}{{AE}}\]
Simplifying, we have:
\[\dfrac{5}{2} = \dfrac{{18}}{{AE}}\]
Solving for AE, we have:
\[AE = \dfrac{2}{5} \times 18\]
\[AE = 7.2cm\]
Hence, the value of AE is 7.2 cm.

Note: You can also prove the similarity by other criteria. The ratio of AD to DB is only given, hence, you can either express AB as AD + DB or you can solve to find the ratio of AB to AD.