Question

In a triangle, ABC, a, c and A are given and m = 2n where m and n are the two possible values of the third side. Prove that $3a=c\sqrt{1+8{{\sin }^{2}}A}$

Answer 1

Hint: Use cosine rule to create a quadratic in b. Use the fact that m and n are the roots of the quadratic. Use the proper that if m,n are the roots of the quadratic equation $a{{x}^{2}}+bx+c=0$ then
$m+n=\dfrac{-b}{a}$ and $mn=\dfrac{c}{a}$ . Compare the two equations to get the above relation.

Complete step-by-step answer:

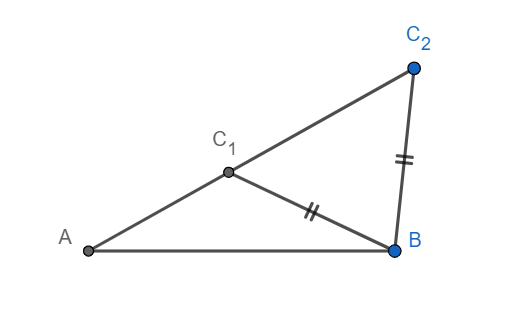
In the diagram above, it can be seen that there are two possible values of AC, viz $A{{C}_{1}}$ and $A{{C}_{2}}$ .
We know that in a $\Delta ABC$
$\cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$
Multiplying both sides by 2bc, we get
$2bc\cos A={{b}^{2}}+{{c}^{2}}-{{a}^{2}}$
Subtracting 2bc cosA from both sides, we get
\[\begin{align}
  & 2bc\cos A-2bc\cos A={{b}^{2}}+{{c}^{2}}-{{a}^{2}}-2bc\cos A \\
 & \Rightarrow {{b}^{2}}+{{c}^{2}}-{{a}^{2}}-2bc\cos A=0 \\
 & \Rightarrow {{b}^{2}}-2bc\cos A+{{c}^{2}}-{{a}^{2}}=0 \\
\end{align}\]
which is a quadratic expression in b whose roots are m and n
Using the property that, the sum of roots $=\dfrac{-b}{a}$ and product of roots $=\dfrac{c}{a}$
So we have
$\begin{align}
  & m+n\text{ }=\text{ }2bc\text{ }cosA \\
 & mn={{c}^{2}}-{{a}^{2}} \\
\end{align}$
Put m = 2n in both equations, we get
$\begin{align}
  & 2n+n\text{ }=\text{ }2c\text{ }cosA \\
 & \Rightarrow 3n=2c\cos A\text{ (i)} \\
 & 2n\left( n \right)={{c}^{2}}-{{a}^{2}} \\
 & \Rightarrow 2{{n}^{2}}={{c}^{2}}-{{a}^{2}}\text{ (ii)} \\
\end{align}$
Squaring equation (i) and dividing (i) by (ii), we get
$\begin{align}
  & \dfrac{9{{n}^{2}}}{2{{n}^{2}}}=\dfrac{4{{c}^{2}}{{\cos }^{2}}A}{{{c}^{2}}-{{a}^{2}}} \\
 & \Rightarrow \dfrac{9}{2}=\dfrac{4{{c}^{2}}{{\cos }^{2}}A}{{{c}^{2}}-{{a}^{2}}} \\
\end{align}$
Cross multiplying we get
$9{{c}^{2}}-9{{a}^{2}}=8{{c}^{2}}{{\cos }^{2}}A$
Adding $9{{a}^{2}}$ on both sides, we get
$9{{c}^{2}}=8{{c}^{2}}{{\cos }^{2}}A+9{{a}^{2}}$
Subtracting $8{{c}^{2}}{{\cos }^{2}}A$ from both sides, we get
$\begin{align}
  & 9{{c}^{2}}-8{{c}^{2}}{{\cos }^{2}}A=8{{c}^{2}}{{\cos }^{2}}A+9{{a}^{2}}-8{{c}^{2}}{{\cos }^{2}}A \\
 & \Rightarrow 9{{a}^{2}}={{c}^{2}}\left( 9-8{{\cos }^{2}}A \right) \\
 & \Rightarrow 9{{a}^{2}}={{c}^{2}}\left( 1+8\left( 1-{{\cos }^{2}}A \right) \right) \\
\end{align}$
Using ${{\sin }^{2}}A=1-{{\cos }^{2}}A$ we get
$9{{a}^{2}}={{c}^{2}}\left( 1+8{{\sin }^{2}}A \right)$
Taking square root on both sides, we get
$3a=c\sqrt{1+8{{\sin }^{2}}A}$

Note: Alternatively you can use the quadratic formula to solve
We have
 $\begin{align}
  & m=\dfrac{2c\cos A+\sqrt{4{{c}^{2}}{{\cos }^{2}}A-4\left( {{c}^{2}}-{{a}^{2}} \right)}}{2} \\
 & =c\cos A+\sqrt{{{c}^{2}}{{\cos }^{2}}A-{{c}^{2}}+{{a}^{2}}} \\
\end{align}$
And $n=c\cos A-\sqrt{{{c}^{2}}{{\cos }^{2}}A-{{c}^{2}}+{{a}^{2}}}$
Given m = 2n
Using we get
$\begin{align}
  & c\cos A+\sqrt{{{c}^{2}}{{\cos }^{2}}A-{{c}^{2}}+{{a}^{2}}}=2\left( c\cos A-\sqrt{{{c}^{2}}{{\cos }^{2}}A-{{c}^{2}}+{{a}^{2}}} \right) \\
 & \Rightarrow c\cos A=3\sqrt{{{c}^{2}}{{\cos }^{2}}A-{{c}^{2}}+{{a}^{2}}} \\
\end{align}$
Squaring both sides, we get
\[\begin{align}
  & {{c}^{2}}{{\cos }^{2}}A=9\left( {{c}^{2}}{{\cos }^{2}}A-{{c}^{2}}+{{a}^{2}} \right) \\
 & \Rightarrow {{c}^{2}}{{\cos }^{2}}A=9{{c}^{2}}{{\cos }^{2}}A-9{{c}^{2}}+9{{a}^{2}} \\
 & \Rightarrow 9{{c}^{2}}-8{{c}^{2}}{{\cos }^{2}}A=9{{a}^{2}} \\
 & \Rightarrow {{c}^{2}}+8{{c}^{2}}\left( 1-{{\cos }^{2}}A \right)=9{{a}^{2}} \\
 & \Rightarrow {{c}^{2}}+8{{c}^{2}}{{\sin }^{2}}A=9{{a}^{2}} \\
\end{align}\]
Taking square root on both sides, we get
$\begin{align}
  & \sqrt{{{c}^{2}}\left( 1+8{{\sin }^{2}}A \right)}=\sqrt{9{{a}^{2}}} \\
 & \Rightarrow c\sqrt{1+8{{\sin }^{2}}A}=3a \\
\end{align}$
Hence proved.
Observe that we chose $m=\dfrac{2c\cos A+\sqrt{4{{c}^{2}}{{\cos }^{2}}A-4\left( {{c}^{2}}-{{a}^{2}} \right)}}{2}$ and not $n=\dfrac{2c\cos A+\sqrt{4{{c}^{2}}{{\cos }^{2}}A-4\left( {{c}^{2}}-{{a}^{2}} \right)}}{2}$ because m>n since m = 2n