Question

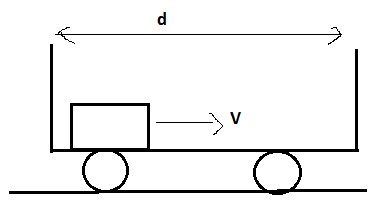
In a smooth stationary cart of length $d$, a small block is projected along its length with velocity $v$ towards front. Coefficient of restitution for each collision is $e$. The cart rests on a smooth ground and can move freely. The time taken by block to come to rest with respect to cart is:

A) $\dfrac{{ed}}{{\left( {1 - e} \right)v}}$
B) $\dfrac{{ed}}{{\left( {1 + e} \right)v}}$
C) $\dfrac{d}{e}$
D) Infinite.

Answer 1

Hint-The value of coefficient of restitution e is independent of the masses and velocities of the colliding bodies. It depends only on the nature of their materials. The forces exerted by each body on the other are equal and opposite, according to Newton’s third law of motion. These forces cause a small change in their shape. This gives rise to elastic forces in the bodies and makes them to rebound with some other velocities.

Complete step by step answer:
Given, length of the stationary cart is $d$, a small block is projected along its length with velocity v towards front and Coefficient of restitution for each collision is e.
During each collision the block moves a distance relative to the cart.
Initial relative velocity$ = v$
Coefficient of restitution$ = e$
${\text{e = }}\dfrac{{{\text{relative velocity of separation after collision}}}}{{{\text{relative velocity of approach before collision}}}}$
If v is the magnitude of velocity with which a small block is projected along its length towards front, then the magnitude of velocity with which it rebounds after first collision$ = ev$
In general relative velocity after n collision$ = v{e^n}$
Time taken can be calculated using,$time = \dfrac{{{\text{distance}}}}{{{\text{velocity}}}} = \dfrac{d}{v}$
So, total time when relative velocity becomes zero$ = \sum\limits_{n = 0}^n {\dfrac{{{d_n}}}{{{v_n}}}} $ …………….(1)
Where,${d_n}$ is distance travelled for each round of collision and ${v_n} = v{e^n}$
Substitute in equation (1), we get
Total time$ = \left[ {\dfrac{d}{v} + \dfrac{d}{{ev}} + \dfrac{d}{{{e^2}v}} + \dfrac{d}{{{e^3}v}} + ............} \right]$
Take common outside,
$T = \dfrac{d}{v} \times \left[ {\dfrac{1}{1} + \dfrac{1}{e} + \dfrac{1}{{{e^2}}} + \dfrac{1}{{{e^3}}} + ............} \right]$
Can be written as,
$T = \dfrac{d}{v} \times \left[ {1 + \dfrac{1}{e} + \dfrac{1}{{{e^2}}} + \dfrac{1}{{{e^3}}} + ............} \right]$
Above equation is in geometric progression, then $r = \dfrac{1}{e} > 1$
$\because e < 1$
Hence, total time=infinite.

$\therefore $ Correct option is (D).

Additional information:
-Coefficient of restitution has no unit and no dimensions.
-For a perfectly elastic collision, e=1
-For a perfectly inelastic collision, e=0
-For the rest of the collisions, e lies between 0 and 1.

Note:If V is the magnitude of velocity with which the ball hits the ground, then the magnitude of velocity with which it rebounds after first collision from the ground is${V_1}$
As we know, ${\text{e = }}\dfrac{{{\text{relative velocity of separation after collision}}}}{{{\text{relative velocity of approach before collision}}}}$
$e = \dfrac{{{V_1}}}{V}$
$ \Rightarrow {V_1} = eV$
The magnitude of velocity with which the ball rebounds from the ground after second collision is
\[{V_2} = e{V_1}\]
\[ \Rightarrow {V_2} = e(eV)\]
\[\therefore {e^2}V\]
Similarly, the magnitude of the velocity with which the ball rebounds from the ground after${n^{th}}$ collision is, ${V_n} = e{V_{n - 1}}$
$ \Rightarrow {V_n} = e({e^{n - 1}}V)$
$ \Rightarrow {e^n}V$
$\therefore {V_n} = {e^n}V$