Question

In a right-angled triangle $\Delta ABC$, the lengths of two sides are 8 cm and 6 cm, then which among the given statements is/are correct?

(a) Length of greatest side is 10 cm
(b) Angle ACB is greater than ${{90}^{\circ }}$
(c) Angle BAC is less than ${{90}^{\circ }}$
(d) Pythagoras theorem is not applicable here.

Answer 1

Hint: Assume that the sides AB and BC are of length 8 cm and 6 cm respectively. Now, apply Pythagoras theorem: $hypotenuse=\sqrt{perpendicula{{r}^{2}}+bas{{e}^{2}}}$ by considering the side AC as hypotenuse to determine its length.

Complete step by step answer:

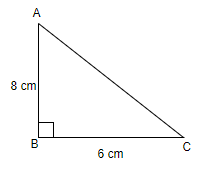
From the figure, it is clear that side AC is the hypotenuse of the given right angle triangle because it is opposite to the vertex containing right angle. We know that hypotenuse is the greatest side of a right angle triangle. Let us determine its length.
Here, we are assuming the sides AB and BC are of length 8 cm and 6 cm respectively. Therefore, applying Pythagoras theorem: $hypotenuse=\sqrt{perpendicula{{r}^{2}}+bas{{e}^{2}}}$, we get,
\[\begin{align}
  & AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}} \\
 & =\sqrt{{{8}^{2}}+{{6}^{2}}} \\
 & =\sqrt{64+36} \\
 & =\sqrt{100} \\
 & =10 \\
\end{align}\]
Therefore, the length of hypotenuse is 10 cm. Hence, option (a) is correct.
Now, we know that, in a triangle, there cannot be two right angles or two obtuse angles because the sum of all the three internal angles is ${{180}^{\circ }}$.
Since, angle ABC is ${{90}^{\circ }}$, therefore, the other two angles must be less than ${{90}^{\circ }}$. Therefore, angle BAC and angle ACB should be less than ${{90}^{\circ }}$.
Hence, option (c) is correct.

So, the correct answers are “Option a and c”.

Note: One may note that, here we have assumed the length of side AB as 8 cm and length of side BC as 6 cm. you can assume its opposite also. This will not change the length of hypotenuse AC. Pythagoras theorem is applicable for all existing right angle triangles. Also, for a triangle to exist, if one of its angles is ${{90}^{\circ }}$ or an obtuse angle, then the other two angles must be acute angles.