Question

In a rhombus \[ABCD\],\[\angle ABC = {56^ \circ }\] , then what will be the measure of\[\angle ACD\]

Answer 1

Hint:In this question, we are provided with one of the angles of the rhombus\[\square
ABCD\]. By using the properties of opposite angles of the rhombus and some general mathematical operations we’ll find the measure of\[\angle ACD\].

Complete step by step solution:

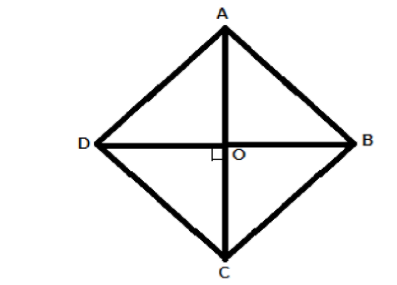
We are provided with measure of \[\angle ABC = {56^ \circ }\]
One of the properties of the rhombus states that the opposite angles of a rhombus are congruent.

Applying the above mentioned property,
\[
\angle ABC = \angle ADC \\
\therefore \angle ADC = {56^ \circ } \\
\]
One of the properties of rhombus states that the diagonals of a rhombus bisect each other.
As shown in the diagram, in \[\vartriangle OCD\]
The sum of measure of all angles of a triangle is \[{180^ \circ }\], which implies,
\[
\angle OCD + \angle ODC + \angle COD = {180^ \circ } \\
\Rightarrow \angle OCD + {28^ \circ } + {90^ \circ } = {180^ \circ } \\
\Rightarrow \angle OCD + {118^ \circ } = {180^ \circ } \\
\Rightarrow \angle OCD = {180^ \circ } - {118^ \circ } \\

\Rightarrow \angle OCD = {62^ \circ } \\
\]
The points A and O lie on the same line.
Therefore, \[\angle ACD = {62^ \circ }\]

Additional information:Rhombus is a special kind of quadrilateral. A quadrilateral is a polygon having four angles, four vertices and four sides. The opposite sides of the rhombus are parallel and the opposite angles of the rhombus are equal. The diagonals of the rhombus bisect each other and form a right angle.

The addition of two adjacent angles of a rhombus is 180 degrees. When the two diagonals of the rhombus bisect each other it forms 4 right angled triangles. These right angles triangles are congruent to each other. Rhombus can also act as a parallelogram as the opposite sides of the rhombus area parallel.

Note:It is to be noted that the sides of the rhombus are named in an orderly manner. If the sides of the rhombus are named randomly in a distorted manner then the two given angles may not become adjacent angles and the approach would be considered wrong. So care should be taken for naming the given rhombus and then identifying the angles given in the problem to solve it.