Question

In a quadrilateral \[ABCD\], which is not a trapezium. It is known that $\angle DAB = \angle ABC = 60^\circ $. Moreover, $\angle CAB = \angle CBD$. Then
A. $AB = BC + CD$
B. $AB = AD + CD$
C. $AB = BC + AD$
D. $AB = AC + AD$?

Answer 1

Hint: Here in the given question, we are given that in a quadrilateral \[ABCD\], which is not a trapezium (it means its bases are not parallel to each other). In the quadrilateral, $\angle DAB = \angle ABC = 60^\circ $ and $\angle CAB = \angle CBD$. We will first draw a diagram using the information given in the question.

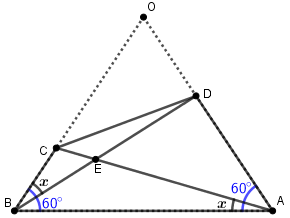
Now, we have quadrilateral \[ABCD\], which is not a trapezium. If sides $AD$ and $BC$ are extended the $\vartriangle ABO$, equilateral triangle is formed. As mentioned in the question, $\angle CAB = \angle CBD$. So, let $\angle CAB = \angle CBD = x$. Now we will solve the given question using the law of sines. The law of sines is defined as the ratio of side length to the sine of the opposite angle. It holds for all the three sides of a triangle respective of their sides and angles. Law of sines: $\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}$.

Complete step by step answer:
Now we will apply law of sines in $\vartriangle ABC$, we have

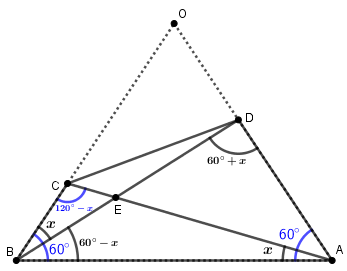
$\dfrac{{AB}}{{\sin \angle ACB}} = \dfrac{{BC}}{{\sin \angle CAB}} = \dfrac{{AC}}{{\sin \angle ABC}}$
As we know, the sum of interior angles of a triangle is $180^\circ $. Therefore, we get
\[\angle ACB + \angle CAB + \angle ABC = 180^\circ \]
As we know, $\angle ABC = 180^\circ $ and $\angle CAB = x$. Therefore, we get
\[\angle ACB + x + 60^\circ = 180^\circ \]
\[\angle ACB = 180^\circ - 60^\circ - x\]
On subtraction, we get
\[\angle ACB = 120^\circ - x\]
On substituting the value of angles, we get
$\dfrac{{AB}}{{\sin \left( {120^\circ - x} \right)}} = \dfrac{{BC}}{{\sin x}} = \dfrac{{AC}}{{\sin 60^\circ }}.....\left( i \right)$
Now we will solve $\sin \left( {120^\circ - x} \right)$. As we know $\sin \theta = \sin \left( {180^\circ - \theta } \right)$, so let $\theta = \left( {120^\circ - x} \right)$. From here, we get
$ \Rightarrow \sin \left( {120^\circ - x} \right) = \sin \left( {180^\circ - \left( {120^\circ - x} \right)} \right)$
$ \Rightarrow \sin \left( {120^\circ - x} \right) = \sin \left( {180^\circ - 120^\circ + x} \right)$
On subtraction, we get
$ \Rightarrow \sin \left( {120^\circ - x} \right) = \sin \left( {60^\circ + x} \right)$
As we know $\dfrac{{AB}}{{\sin \left( {120^\circ - x} \right)}} = \dfrac{{BC}}{{\sin x}}$. (From $\left( i \right)$). Therefore, on substituting the value of $\sin \left( {120^\circ - x} \right)$, we get
$ \Rightarrow \dfrac{{AB}}{{\sin \left( {60^\circ + x} \right)}} = \dfrac{{BC}}{{\sin x}}$
$ \Rightarrow BC = AB.\dfrac{{\sin x}}{{\sin \left( {60^\circ + x} \right)}}$
As we know $\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$. Using this, we get
$ \Rightarrow BC = AB.\dfrac{{\sin x}}{{\sin 60^\circ \times \cos x + \cos 60^\circ \times \sin x}}$
As we know $\sin 60^\circ = \dfrac{{\sqrt 3 }}{2}$ and $\cos 60^\circ $. On substituting these values, we get
$ \Rightarrow BC = AB.\dfrac{{\sin x}}{{\dfrac{{\sqrt 3 }}{2} \times \cos x + \dfrac{1}{2} \times \sin x}}$
Now we will apply law of sines in $\vartriangle ABD$, we have
$\dfrac{{AB}}{{\angle ADB}} = \dfrac{{AD}}{{\angle ABD}} = \dfrac{{BD}}{{\angle BAD}}$
Now will find the interior angles of $\vartriangle ABD$. As we know $\angle ABC = \angle ABD + \angle CBD = 60^\circ $ and $\angle CBD = x$. Therefore,
\[ \Rightarrow \angle ABD + x = 60^\circ \]
\[ \Rightarrow \angle ABD = 60^\circ - x\]
Now we will find \[\angle ADB\]. As we know, $\angle ABD = 60^\circ - x$ and $\angle BAD = 60^\circ $.
As we know sum of interior angles of a triangle is $180^\circ $. Therefore, we get
\[\angle ADB + \angle ABD + \angle BAD = 180^\circ \]
On substituting values of angles, we get
 \[ \Rightarrow \angle ADB + 60^\circ - x + 60^\circ = 180^\circ \]
\[ \Rightarrow \angle ADB = 180^\circ - 120^\circ + x\]
On subtraction, we get
\[ \Rightarrow \angle ADB = 60^\circ + x\]
On substituting value of angles, we get
$\dfrac{{AB}}{{\sin \left( {60^\circ + x} \right)}} = \dfrac{{AD}}{{\sin \left( {60^\circ - x} \right)}} = \dfrac{{BD}}{{\sin 60^\circ }}.....\left( {ii} \right)$
$ \Rightarrow \dfrac{{AB}}{{\sin \left( {60^\circ + x} \right)}} = \dfrac{{AD}}{{\sin \left( {60^\circ - x} \right)}}$
$ \Rightarrow AD = AB \times \dfrac{{\sin \left( {60^\circ - x} \right)}}{{\sin \left( {60^\circ + x} \right)}}$
As we know $\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$ and $\sin \left( {A - B} \right) = \sin A\cos B - \cos A\sin B$. Therefore, we get
\[ \Rightarrow AD = AB \times \dfrac{{\sin 60^\circ \times \cos x - \cos 60^\circ \times \sin x}}{{\sin 60^\circ \times \cos x + \cos 60^\circ \times \sin x}}\]
As we know $\sin 60^\circ = \dfrac{{\sqrt 3 }}{2}$ and $\cos 60^\circ $. On substituting these values, we get
$ \Rightarrow AD = AB \times \dfrac{{\dfrac{{\sqrt 3 }}{2} \times \cos x - \dfrac{1}{2} \times \sin x}}{{\dfrac{{\sqrt 3 }}{2} \times \cos x + \dfrac{1}{2} \times \sin x}}$
Now we will add $BC + AD$.
$ \Rightarrow BC + AD = AB.\dfrac{{\sin x}}{{\dfrac{{\sqrt 3 }}{2} \times \cos x + \dfrac{1}{2} \times \sin x}} + AB.\dfrac{{\dfrac{{\sqrt 3 }}{2} \times \cos x - \dfrac{1}{2} \times \sin x}}{{\dfrac{{\sqrt 3 }}{2} \times \cos x + \dfrac{1}{2} \times \sin x}}$
Take $AB$ as a common term.
$ \Rightarrow BC + AD = AB \times \left( {\dfrac{{\sin x}}{{\dfrac{{\sqrt 3 }}{2} \times \cos x + \dfrac{1}{2} \times \sin x}} + \dfrac{{\dfrac{{\sqrt 3 }}{2} \times \cos x - \dfrac{1}{2} \times \sin x}}{{\dfrac{{\sqrt 3 }}{2} \times \cos x + \dfrac{1}{2} \times \sin x}}} \right)$
Take LCM
$ \Rightarrow BC + AD = AB \times \left( {\dfrac{{\sin x + \dfrac{{\sqrt 3 }}{2} \times \cos x - \dfrac{1}{2} \times \sin x}}{{\dfrac{{\sqrt 3 }}{2} \times \cos x + \dfrac{1}{2} \times \sin x}}} \right)$
$ \Rightarrow BC + AD = AB \times \left( {\dfrac{{\dfrac{{\sqrt 3 }}{2} \times \cos x + \dfrac{{2\sin x - \sin x}}{2}}}{{\dfrac{{\sqrt 3 }}{2} \times \cos x + \dfrac{1}{2} \times \sin x}}} \right)$
On subtraction of terms in numerator, we get
$ \Rightarrow BC + AD = AB \times \left( {\dfrac{{\dfrac{{\sqrt 3 }}{2} \times \cos x + \dfrac{{\sin x}}{2}}}{{\dfrac{{\sqrt 3 }}{2} \times \cos x + \dfrac{1}{2} \times \sin x}}} \right)$
On canceling common terms, we get
$ \Rightarrow BC + AD = AB \times \left( {\dfrac{{\dfrac{{\sqrt 3 }}{2} \times \cos x + \dfrac{1}{2} \times \sin x}}{{\dfrac{{\sqrt 3 }}{2} \times \cos x + \dfrac{1}{2} \times \sin x}}} \right)$
On canceling out common terms, we get
$ \Rightarrow BC + AD = AB \times 1$
On multiplication, we get
$ \Rightarrow BC + AD = AB$
$ \Leftrightarrow AB = BC + AD$
Therefore, the correct option is C.

Note:There is another method also to solve the given question.

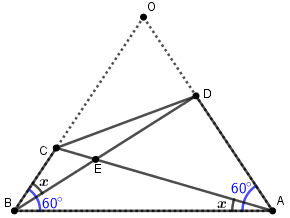
Extend the sides $AD$ and $BC$ to complete the equilateral triangle $\vartriangle ABO$.
Let the side $AB$ be $y$, as we know sides of the equilateral triangle are equal. Therefore, $AB = BO = AO = y$.
Let $AD$ be $a$ and $BC$ be $b$.
Observe that, $\vartriangle ABC \sim \vartriangle BOD$.
(Both triangles are congruent because of ASA property. As we know all angles of the equilateral triangle are of $60^\circ $, so we have $\angle ABC = \angle BOD$. As we know sides are equal, so we have $OB = AB = y$. We also have $\angle OBD = \angle BAC = x$)
So, we have
$\dfrac{{BC}}{{OD}} = \dfrac{{AB}}{{BO}}$
As we supposed $AD$ be $a$. Therefore, $OD = y - a$.
$ \Rightarrow \dfrac{b}{{y - a}} = \dfrac{x}{x}$
On canceling common terms, we get
$ \Rightarrow \dfrac{b}{{y - a}} = 1$
On cross multiplication, we get
$ \Rightarrow y - a = b$
On shifting $a$ to RHS, we get
$ \Rightarrow y = a + b$
As we know $AB = y$, $AD = a$ and $BC = b$. Therefore, we get
$ \Rightarrow AB = BC + AD$.