Question

In a quadrilateral ABCD, the point P divides DC in the ratio 1:2 and Q is the midpoint of AC. If AB+2AD+BC−2DC=kPQ, then k is equal to:
1) -6
2) -4
3) 6
4) 4

Answer 1

Hint: We are given a quadrilateral ABCD, where P divides DC in the ratio 1:2 and Q is the midpoint of AC. Thus, according to this given information, we will first draw the diagram. Then, we will solve the LHS part of the given equation with the help of the diagram. And, lastly substitute this value in the equation and compare both the LHS and RHS to get the final value of k.

Complete answer:
Given that,
In a quadrilateral ABCD, point P divides DC in the ratio 1:2
\[DC = \dfrac{3}{2}PC\]
And, point Q is the midpoint of AC.
According to the given information, we will draw a diagram as below:

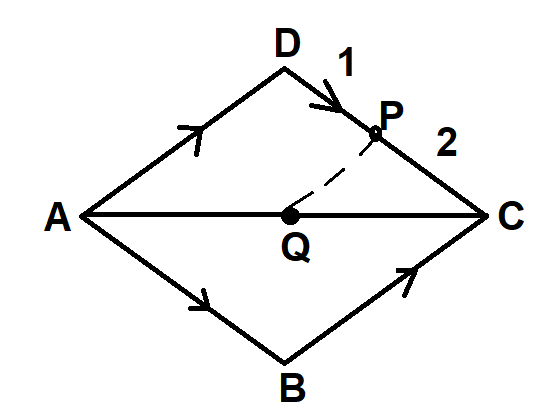
We are given that,
\[AB + 2AD + BC - 2DC = kPQ\]
Here, we will solve the LHS first and then substitute the value in the given equation to get the value of k.
LHS
\[ = AB + 2AD + BC - 2DC\]
Rearranging this expression, we will get,
\[ = (AB + BC) + 2AD - 2DC\]
We, know that, AB+BC = AC and AD= AC+CD
\[ = AC + 2(AC + CD) - 2DC\]
Removing the brackets, we get,
\[ = AC + 2AC + 2CD - 2DC\]
\[ = 3AC - 2DC - 2DC\]
\[ = 3AC - 4DC\]
Since, Q is the midpoint of AC.
\[\therefore AQ = QC\]
\[ \Rightarrow AC = 2QC\]
Substituting the value of AC and DC, we will get,
\[ = 3(2QC) - 4(\dfrac{3}{2}PC)\]
Now on doing the simplification,
\[ = 6QC - 6PC\]
\[ = 6QC + 6CP\]
Now again on doing the simplification,
\[ = 6(QC + CP)\]
\[ = 6QP\]
\[ = - 6PQ\]
Now, we will substitute this value in the given equation, we will get,
\[ \Rightarrow - 6PQ = kPQ\]
\[ \Rightarrow - 6 = k\]
\[ \Rightarrow k = - 6\]
Hence, for a given quadrilateral ABCD, if \[AB + 2AD + BC - 2DC = kPQ\] then the value of \[k = - 6\].

Note:
A quadrilateral is a plane figure that has four sides or edges, and also have four corners or vertices. As the word ‘Quad’ means four, all these types of a quadrilateral have four sides, and the sum of angles of these shapes is 360 degrees like, Trapezium, Parallelogram, Squares, Rectangle, Rhombus and Kite.