Question

In a plot of log k vs $\dfrac{1}{T}$ the slope is:
(a)- $\dfrac{-{{E}_{a}}}{2.303}$
(b)- $\dfrac{{{E}_{a}}}{2.303R}$
(c)- $\dfrac{{{E}_{a}}}{2.303}$
(d)- $\dfrac{-{{E}_{a}}}{2.303R}$

Answer 1

Hint: The equation called Arrhenius equation is usually written as $k=A{{e}^{-{{E}_{a}}/RT}}$ where the pre-exponential factor A is a constant and is called frequency factor and${{E}_{a}}$ is called the activation energy, R is the gas constant and T is the temperature. The activation energy is calculated by the formula $\log \dfrac{{{k}_{2}}}{{{k}_{1}}}=\dfrac{{{E}_{a}}}{2.303R}\left[ \dfrac{{{T}_{2}}-{{T}_{1}}}{{{T}_{2}}{{T}_{1}}} \right]$ where ${{k}_{1}}\text{ and }{{k}_{2}}$ are rate constants at different temperatures.


Complete step by step answer:
The Arrhenius equation is usually written as$k=A{{e}^{-{{E}_{a}}/RT}}$.
And its log form is:
$\log\dfrac{{{k}_{2}}}{{{k}_{1}}}=\dfrac{{{E}_{a}}}{2.303R}\left[ \dfrac{{{T}_{2}}-{{T}_{1}}}{{{T}_{2}}{{T}_{1}}} \right]$
To test the validity of the Arrhenius equation, let us consider the equation as:

$\ln k=-\dfrac{{{E}_{a}}}{RT}+\ln A$
Or it can be converted into:
$\log k=-\dfrac{{{E}_{a}}}{2.303RT}+\log A$
This equation can be written in the form of the equation of the straight line.
The equation of the straight line is: $y=mx\text{ + }c$
So, in the straight line equation, when we plot a graph between y and x, we get m as the slop.
Similarly when we plot the graph for the equation $\log k=-\dfrac{{{E}_{a}}}{2.303RT}+\log A$:
$\log k$ is the y and $\dfrac{1}{T}$is the x, the validity of the equation is confirmed.
So, when we plot the graph we get m = $\dfrac{-{{E}_{a}}}{2.303R}$
So, the slope of the line = $\dfrac{-{{E}_{a}}}{2.303R}$
The graph of log k vs $\dfrac{1}{T}$ is given below:

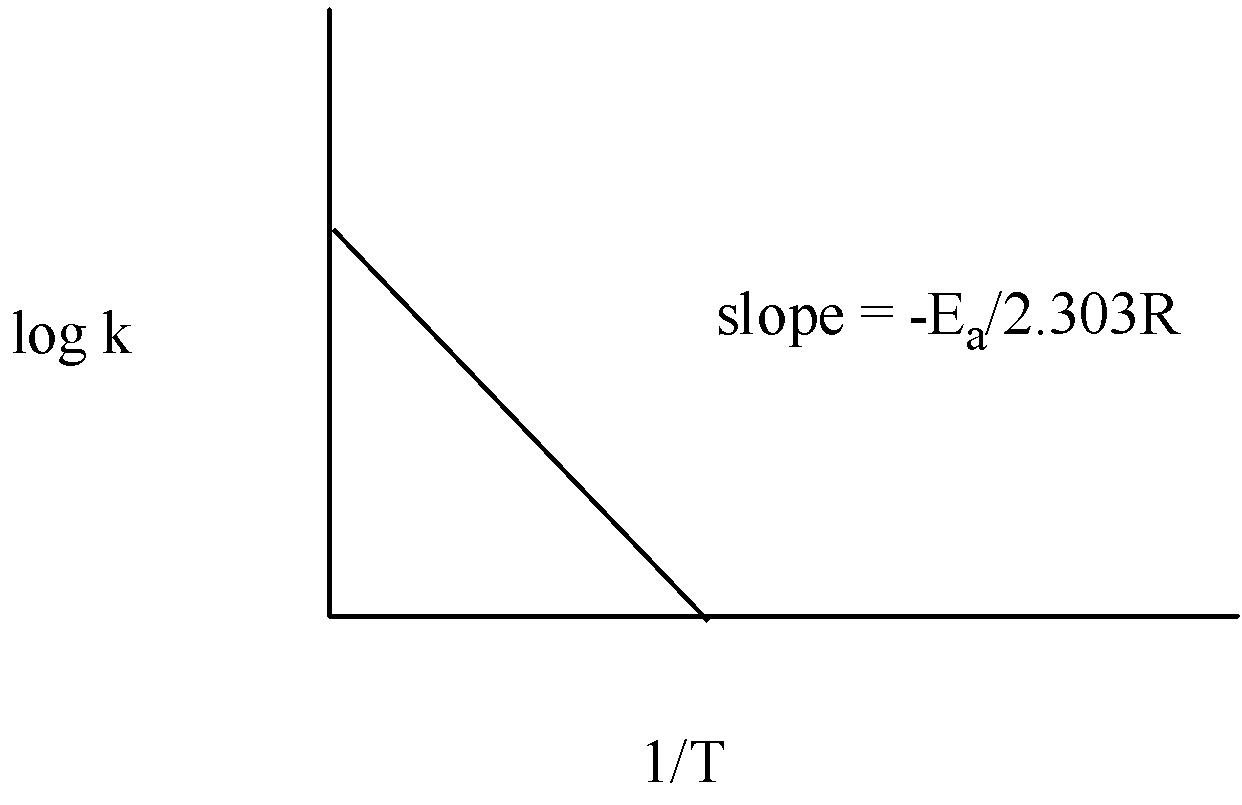
Thus, measuring the slope of the line, the value of ${{E}_{a}}$ can be calculated.
So, the correct answer is “Option D”.

Note: If we plot a straight line graph for the equation $\ln k=-\dfrac{{{E}_{a}}}{RT}+\ln A$, the y will be ln k and the x will be $\dfrac{1}{T}$ so in this case we get the slope of$-\dfrac{{{E}_{a}}}{R}$. so, by converting any equation to the straight-line equation we can find the slope of the equation.