Question

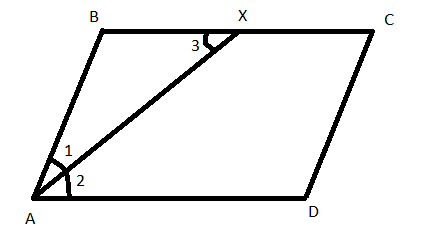
In a parallelogram ABCD, the bisector of \[\angle {\rm{A}}\] also bisects BC at X. Prove that \[{\rm{AD = 2AB}}\]

Answer 1

Hint: Here in this question we have to use the basic concepts of the parallelogram and bisectors. So by using the different basic theorems of angle we will make the two angle of the triangle ABX equal and then by that we will get a relation of the side of the triangle and then by simplifying and modifying the equation of the sides of triangle ABX according to what we need to prove then we will get the answer.

Complete step-by-step answer:
ABCD is a given parallelogram with side AD parallel to BC i.e. \[{\rm{AD}}\parallel {\rm{BC}}\] and side AB parallel to CD i.e. \[{\rm{AB}}\parallel {\rm{CD}}\]
It is given that a bisector bisects the angle\[\angle {\rm{A}}\]. So the angle is bisected into two equal half angles i.e. \[\angle {\rm{1\& }}\angle {\rm{2}}\] where\[\angle {\rm{1 = }}\angle {\rm{2}}\]………. (1)
This bisector also bisects the side BC at X i.e.\[{\rm{BX = XC}}\].
Now by using the concept of alternate interior angles which states that between two parallel lines when a transversal line is present so the interior angles formed by it are equal to each other.
Therefore, we get \[\angle {\rm{2 = }}\angle {\rm{3}}\]………. (2)
So from equation (1) and equation (2), we get
\[ \Rightarrow \angle {\rm{1 = }}\angle 3\]
Now we will take the triangle to form an equation in terms of sides of the triangle.
We know that if the two angles of a triangle are equal then the sides opposite to them are always equal. So, we get
\[ \Rightarrow {\rm{AB = BX}}\]
Now we can write this as
\[ \Rightarrow {\rm{2AB = 2BX}}\]
As X is the midpoint of line BC so \[{\rm{BX = XC}}\]. Therefore, we get
\[ \Rightarrow {\rm{2AB = 2BX = BX + BX = BX + XC}}\]
\[ \Rightarrow {\rm{2AB = BC}}\]
\[{\rm{AD = BC}}\] as these are the parallel opposite sides of the parallelogram. So, we get
\[ \Rightarrow {\rm{2AB = AD}}\] or we can write it as
\[ \Rightarrow {\rm{AD = 2AB}}\]
Hence proved

Note: Geometry is the branch of mathematics that deals with points, lines and shapes. In geometry, bisection is the division of something into two equal parts. Bisection is generally done with a line which is called a bisector. There are two main types of bisectors i.e. line segment bisector and angle bisector.
A line segment bisector is a line or line segment that divides the line into two equal parts or which passes through the midpoint of the line segment.
Angle bisector is the line or line segment that divides an angle into two equal parts. An angle has only one bisector. Also there are two types of angle bisectors i.e. interior and exterior angle bisector.
Vertically Opposite Angles (vertical angles) are the angles opposite each other when two lines intersect or cross each other and pairs of vertically opposite angles (vertical angles) are always equal to each other.