Question

In a male population of 1000, the mean height is 68.16 inches and the standard deviation is 3.2 inches. How many men can be more than 6 feet (72 inches) $P\left( z<1.2 \right)=0.8849$

Answer 1

Hint: To solve this question, we should know the concept of normal distribution. We will assume that the distribution of the population follows normal distribution. For a normal distribution in x having a of mean $\mu $ and standard deviation $\sigma $, we can write the probability as $P\left( x>{{x}_{1}} \right)=P\left( z>\dfrac{{{x}_{1}}-\mu }{\sigma } \right)$ where z is the standard normal variable. We can get the value of $P\left( z>\dfrac{{{x}_{1}}-\mu }{\sigma } \right)$ from the standard normal table.

Complete step-by-step solution

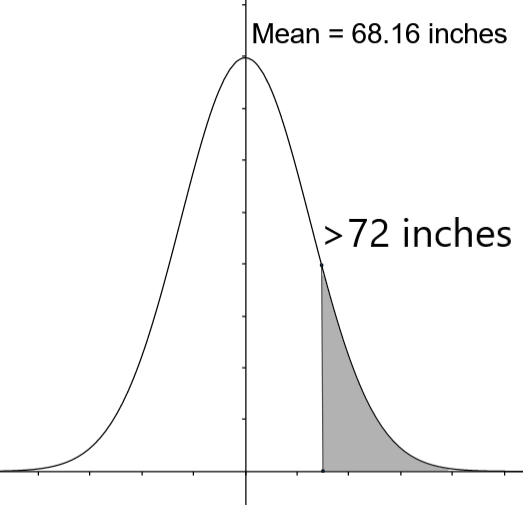
$\sigma =3.2$ We are given a population of 1000 men and the mean height of them is 68.16 inches and the standard deviation is 3.2 inches. Generally, the population data follows the normal distribution. Here, we can apply the properties of the normal distribution for the population data that we have. We are asked to find the area of the shaded region of the figure.
For a normal distribution in x having a of mean $\mu$ and standard deviation $\sigma $, we can convert the normal random variable into standard normal random variable z using the relation
$z=\dfrac{x-\mu }{\sigma }$
We have the values as
$\mu =68.16$
We need to find the value of z at the position where $x=72$. Using these values, we get
$z=\dfrac{72-68.16}{3.2}=\dfrac{3.84}{3.2}=\dfrac{3.2\times 1.2}{3.2}=1.2$
We are asked to find the value of $P\left( z> 1.2 \right)$
We know that the total probability is 1. Using this, we can write that
$P\left( z <1.2 \right)+P\left( z> 1.2 \right)=1$
We are given that $P\left( z< 1.2 \right)=0.8849$. Using this, we get
$\begin{align}
  & 0.8849+P\left( z>1.2 \right)=1 \\
 & P\left( z>1.2 \right)=1-0.8849=0.1151 \\
\end{align}$
We should multiply this value to the total population to get the value of the number of persons. We get the required number as
Number of male greater than 6 feet is $=1000\times P\left( z>1.2 \right)=1000\times 0.1151=115$
$\therefore $ The required number of male population is 115.

Note: They can ask a question by not mentioning the required value of probability of standard normal value. In such cases, we should remember some standard values of the standard normal table. They are
$\begin{align}
  & P\left( z<1 \right)=0.8413 \\
 & P\left( z<2 \right)=0.9772 \\
 & P\left( -1< z< 1 \right)=0.6826 \\
\end{align}$
Using these values, we can get an approximate answer when there is no value given.