Question

In a group of \[{\mathbf{45}}\] students, \[{\mathbf{22}}\] can speak Hindi only, \[{\mathbf{12}}\] can speak English only. How many can speak both Hindi and English?

Answer 1

Hint: In the given question we have to find out the number of students speaking both Hindi and English. To solve this question let us consider the number of students speaking Hindi is $(22 + x)$ as no. of people speaking both are also included in people of speak Hindi whereas the number of students speaking English is $\left( {12 + x} \right)$ as no. of people speaking both are also included in people of speak English . Use the relation $n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)$ and work out the value of to get the answer. This question can be solved using the Venn diagram.

Complete step-by-step answer:

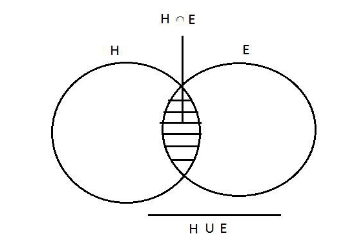
Let, number of students speaking English is $\left( {12 + x} \right)$
i.e. $n\left( E \right) = 12 + x$
& let, number of students speaking Hindi is \[\left( {22 + x} \right)\]
i.e. \[n(H) = 22 + x\]
Where \[x\] are the number of students who can speak both English and Hindi
Since, total no. of students are \[45\]
i.e. \[n\left( {A \cup B} \right) = 45\]
We know the relation –
\[{
  n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right) \\
  here, \\
  n\left( {H \cup E} \right) = n\left( H \right) + n\left( E \right) - n\left( {H \cap E} \right) \\
   \Rightarrow 45 = 22 + x + 12 + x - x \\
   \Rightarrow 45 = 34 + x \\
   \Rightarrow x = 11 \\
} \]
\[\therefore 11\] students can speak both English and Hindi.

Note: The asked question was related to set theory. This question can be solved by using the Venn Diagram. Set theory is the collection of sets on objects. Questions related to them can be solved by using Venn diagrams or set theory approach.