Question

In a group of 70 people, 31 speak Hindi, 33 speak Bengali, 32 speak Telugu, 16 speak both Hindi and Bengali, 14 speak both Hindi and Telugu, 15 speak Bengali and Telugu, 5 persons can not speak any of the three languages. Find out how many can speak all the languages.
A. 21
B. 25
C. 14
D. 51

Answer 1

Hint: In this question, we must draw the Venn diagram first, consisting of three circles of Hindi, Bengali, and Telugu language speakers. Now solve it by using the given information and find the people who speak all the three languages.

Complete step-by-step answer:
We are given that in a group of 70 people, 31 speak Hindi, 33 speak Bengali, 32 speak Telugu, 16 speak both Hindi and Bengali, 14 speak both Hindi and Telugu, 15 speak Bengali and Telugu, 5 persons cannot speak any of the three languages. Here, we have to find the number of persons who speak all the three languages.

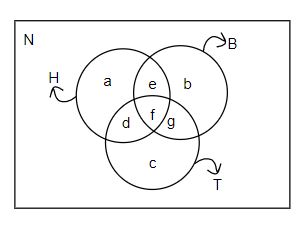
In the above figure, we have made a Venn diagram which represents the group of 70 people, who speak different languages. The first circle H represents the number of all the Hindi speakers. The second circle B represents the number of all the Bengali speakers. The third circle T represents the number of all the Telugu speakers.
Here, a, b, c represent the number of people who speak only one language, which is either Hindi or Bengali or Telugu. And e, d, and g represents the number of people who speak two languages.
e represents the number of people who speak Hindi and Bengali.
d represents the number of people who speak Hindi and Telugu.
g represents the number of people who speak Bengali and Telugu.
f represents the number of people who speak all the three languages.
N represents the number of people who cannot speak any of the three languages. We have been given that there are a total of 70 people, so we get,
N + a + b + c + d + e + f + g = 70 ……….(i)
We are given that 31 people speak Hindi, 33 speak Bengali and 32 speak Telugu, so we get,
H = a + e + d + f = 31 ……….(ii)
B = e + b + f + g = 33 ……….(iii)
T = d + f + g + c = 32 ……….(iv)
We are also given that 16 speak both Hindi and Bengali, so we get,
f + e = 16, so e = 16 - f
Also, 15 speak Bengali and Telugu and 14 speak Hindi and Telugu, so we get,
f + g = 15, so, g = 15 - f
f + d = 14, so, d = 14 - d
Also, there are 5 people who can’t speak any of these languages, so we get, N = 5
By substituting the values of d, e, g and N in equation (i), we get,
5 + a + b + c + f + (16 - f) + (14 - f) + (15 - f) = 70
a + b + c - 2f = 70 - 5 - 16 -14 - 15
a + b + c - 2f = 70 - 50
a + b + c - 2f = 20 ……….(v)
Now, by adding equations (ii), (iii), (iv), we get,
(a + e + d + f) + (e + b + f + g) + (d + f + g + c) = 31 + 32 + 33
By rearranging the above equation, we get,
(a + b + c) + 3f + 2(e + d +g) = 96
By substituting the values e, d, and g, we get,
(a + b + c) + 3f + 2(14 - f + 15 - f + 16 - f) = 96
(a + b + c) - 3f + 2(45) = 96
(a + b + c) - 3f = 96 - 90
(a + b + c) - 3f = 6 ……….(vi)
By subtracting equation (v) from equation (vi), we get,
[((a + b + c) - 3f] - [(a + b + c) - 2f] = 6 - 20
By cancelling the like terms, we get,
-3f + 2f = - 14
So, f = 14
Therefore, we get the number of people who speak all the three languages as 14. So, option C is the correct answer.

Note: In this question students can directly get the answer by using the formula of, $A\cup B\cup C=(A+B+C)-(A\cap B+B\cap C+A\cap C)+(A\cap B\cap C)$. Here we have to find $A\cap B\cap C$ and we have been given A = 31, B = 33, C = 32 and $A\cap B=16,B\cap C=14$ and $A\cap C=15$ and $A\cup B\cup C=70-5=65$. So, we can directly substitute these to find $A\cap B\cap C$.