
In a group of
(i) Played cricket
(ii) Played tennis
(iii) Did not play any of the above three games.
Answer
495.9k+ views
Hint: For answering this question we will use the given information and draw the Venn diagram to represent the information assuming that the common part has
Complete step-by-step solution
Now considering from the information given in the question we have a total of
Let
By using this information we can draw a Venn diagram representing this as shown below:
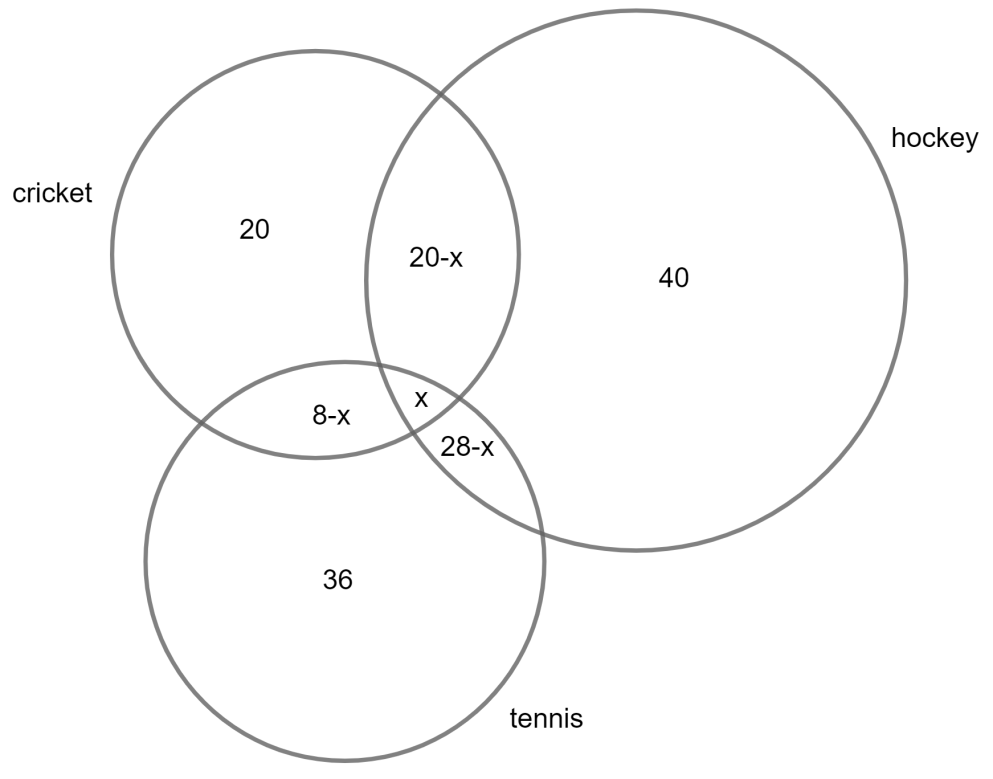
Here, each circle represents the number of students playing the game and the intersection part represents the common students playing both the games.
We have assumed the number of students playing all the 3 sports as
As it is given in the question that the total number of students playing hockey is
By simplifying this we will have
Hence we can say that the total number of students playing cricket will be equal to the sum of all the parts of the circle which is mathematically given as
The number of students who played cricket is
Hence we can say that the total number of students playing tennis will be equal to the sum of all the parts of the circle which is mathematically given as
The number of students who played cricket is
The total number of students who did not play any of the above three games is the difference of the total number of students in the group from the total number of students who play at least one game which is mathematically given as
Hence we can conclude that the total number of students who did not play any of the above three games is
Note: While answering questions of this type we should be careful while drawing the Venn diagram and be sure with the calculations and we should make a note about the intersection part in every case because it is the repeated part. If we had made a mistake and written the number of students playing both cricket and tennis only that is
Complete step-by-step solution
Now considering from the information given in the question we have a total of
Let
By using this information we can draw a Venn diagram representing this as shown below:

Here, each circle represents the number of students playing the game and the intersection part represents the common students playing both the games.
We have assumed the number of students playing all the 3 sports as
As it is given in the question that the total number of students playing hockey is
By simplifying this we will have
Hence we can say that the total number of students playing cricket will be equal to the sum of all the parts of the circle which is mathematically given as
The number of students who played cricket is
Hence we can say that the total number of students playing tennis will be equal to the sum of all the parts of the circle which is mathematically given as
The number of students who played cricket is
The total number of students who did not play any of the above three games is the difference of the total number of students in the group from the total number of students who play at least one game which is mathematically given as
Hence we can conclude that the total number of students who did not play any of the above three games is
Note: While answering questions of this type we should be careful while drawing the Venn diagram and be sure with the calculations and we should make a note about the intersection part in every case because it is the repeated part. If we had made a mistake and written the number of students playing both cricket and tennis only that is
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

How much is 23 kg in pounds class 11 chemistry CBSE




