Question

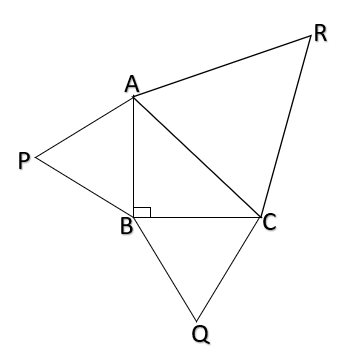
In a given figure equilateral triangles are drawn on the sides of a right triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.

Answer 1

Hint: In this question it is given that 3 equilateral triangles are drawn on sides of the right triangle. Use theorem; ratio of areas of similar triangles is proportional to the square of ratio of their corresponding sides.

Complete step-by-step answer:

Given $\vartriangle PAB,\vartriangle RAC{\text{ and }}\vartriangle BQC{\text{ }}$are equilateral triangles.
To Prove: $Ar(\vartriangle PAB) + Ar(\vartriangle QBC) = Ar(\vartriangle RAC)$
Proof:
Since
$
  \vartriangle PAB,\vartriangle RAC{\text{ and }}\vartriangle BQC{\text{ are equilateral }} \\
  {\text{Hence}} \\
  \vartriangle {\text{PAB}} \sim \vartriangle RAC{\text{ and }}\vartriangle BQC \sim \vartriangle RAC{\text{ [}}\because {\text{they are equiangular]}} \\
$
From
$
  \vartriangle PAB \sim \vartriangle RAC \\
  \dfrac{{Ar(\vartriangle PAB)}}{{Ar(\vartriangle RAC)}} = {\left( {\dfrac{{AB}}{{AC}}} \right)^2}............................(1) \\
$
From
$
  \vartriangle BQC \sim \vartriangle RAC \\
  \dfrac{{Ar(\vartriangle BQC)}}{{Ar(\vartriangle RAC)}} = {\left( {\dfrac{{BC}}{{AC}}} \right)^2}..............................(2) \\
$
Adding (1) and (2) we get,
$
\dfrac{{Ar(\vartriangle PAB)}}{{Ar(\vartriangle RAC)}} + \dfrac{{Ar(\vartriangle BQC)}}{{Ar(\vartriangle RAC)}} = \dfrac{{A{B^2}}}{{A{C^2}}} + \dfrac{{B{C^2}}}{{A{C^2}}} \\
\dfrac{{Ar(\vartriangle PAB) + Ar(\vartriangle BQC)}}{{Ar(\vartriangle RAC)}} = \dfrac{{A{B^2} + B{C^2}}}{{A{C^2}}} \\
  {\text{Using pythagoras theorem to right }}\vartriangle {\text{ABC}} \\
  {\text{A}}{{\text{C}}^2} = A{B^2} + B{C^2} \\
  \dfrac{{Ar(\vartriangle PAB) + Ar(\vartriangle BQC)}}{{Ar(\vartriangle RAC)}} = \dfrac{{A{C^2}}}{{A{C^2}}} = 1 \\
  Ar(\vartriangle PAB) + Ar(\vartriangle BQC) = Ar(\vartriangle RAC) \\
$
Hence Proved.

Note: An equilateral triangle is a triangle in which all three sides are equal. Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in proportion. In other words, similar triangles are the same shape, but not necessarily the same size. Students must remember the criterions for the similarity of triangles