Question

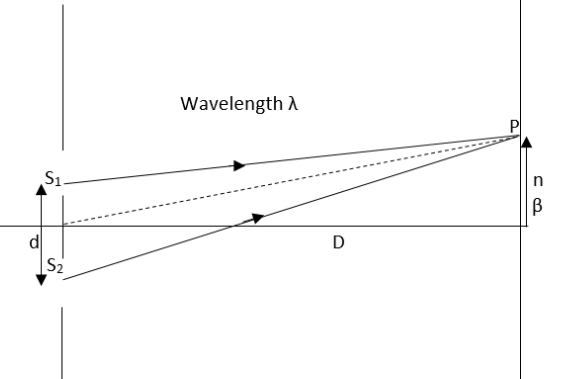
In a double slit experiment, the slits are separated by a distance $d$ and the screen is at a distance $D$ from the slits. Suppose that a maximum has been created just opposite each slit, then calculate the order of the fringe so formed.
$\begin{align}
  & A.\dfrac{{{d}^{2}}}{2\lambda D} \\
 & B.\dfrac{2{{d}^{2}}}{\lambda D} \\
 & C.\dfrac{{{d}^{2}}}{\lambda D} \\
 & D.\dfrac{{{d}^{2}}}{4\lambda D} \\
\end{align}$

Answer 1

Hint: Fringe width is defined as the distance between two successive bright fringes or two successive dark fringes. The fringe width will be a constant for all the fringes, in the interference pattern. Fringe width is not depending on the order of fringe. Fringe width will be directly proportional to wavelength of the light.

Complete step by step answer:
First of all let us mention what all are given in the question. The slits are separated by distance $d$ and the screen is at a distance $D$ from the slits. In this situation mentioned in the question, we can write that,
$\dfrac{d}{2}=n\beta $
The distance between the bright fringe appeared and the dark fringe appeared will be found using the equation given as,
$\beta =\dfrac{D\lambda }{d}$
Substituting the values in the equation will give,
\[\dfrac{d}{2}=n\dfrac{D\lambda }{d}\]
Rearranging the equation in terms of the order of the fringe will give,
\[n=\dfrac{{{d}^{2}}}{2D\lambda }\]

So, the correct answer is “Option A”.

Note: The fringe width in Young's double slit experiment will be increased when the wavelength of the light gets increased. By increasing the distance between the slit also increasing the fringe width. Distance between the screen and the source should be made shorter in order to increase the fringe width. The width of slit can also be increased for the same. Fringe pattern production is defined as the process of projecting a sinusoidal pattern over the surface of a body and using a digital camera, taking the picture of it will give the pattern.