Question

In a continuous printing process, the paper is drawn into the presses at a constant speed $v$. It was found that the winding radius of the roll was reduced by half in a time ${t_1} = 20\min $ of operation. In what time ${t_2}$will the winding radius be reduced by half again?
               

Answer 1

Hint: Try to understand the question with the given diagram first. According to the given case, check for the change in the area in the given time ${t_1}$. Since the speed is constant then the rate of reduction in the area of the circle will be the same. Use it to find the time ${t_2}$.

Complete step-by-step answer:
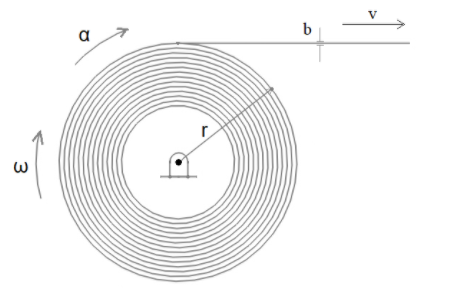
Before solving let’s first try to analyse the given situation here in the problem. You have a roll that is unwinding at a constant rate, i.e. a fixed amount of paper is rolled out in a unit time. In the beginning, the radius of that roll was $'r'$ and after a time ${t_1} = 20\min $, the radius of the roll becomes half, i.e. $\dfrac{r}{2}$. And we have to find out the time ${t_2}$ in which the radius further reduces to half, i.e. becomes$\dfrac{1}{2} \times \dfrac{r}{2} = \dfrac{r}{4}$.
If you’ll consider the figure, which is a side view of that roll we can see that in time, the area of the circle will reduce as$ = \pi {r^2} - \pi {\left( {\dfrac{r}{2}} \right)^2} = \dfrac{3}{4}\pi {r^2}$
Therefore the roll lost an area of $\dfrac{3}{4}\pi {r^2}$ when the radius becomes $\dfrac{r}{2}$ from $r$ in time ${t_1} = 20\min $.
Similarly, area reduced in time ${t_2}$ when the radius goes from $\dfrac{r}{2}$ to $\dfrac{r}{4}$ will be:
$ \Rightarrow \pi {\left( {\dfrac{r}{2}} \right)^2} - \pi {\left( {\dfrac{r}{4}} \right)^2} = \dfrac{{\pi {r^2}}}{4} - \dfrac{{\pi {r^2}}}{{16}} = \dfrac{3}{{16}}\pi {r^2}$
So, the area reduced in time ${t_2}$ when radius changes from $\dfrac{r}{2}$ to $\dfrac{r}{4}$ will be $\dfrac{3}{{16}}\pi {r^2}$
Since paper is unwounded at a constant speed the rate of reduction of area of the circle will also be the same.
We know that, area of $\dfrac{3}{4}\pi {r^2}$ reduced in $20\min $
$ \Rightarrow $ An area of $\dfrac{1}{4} \times \dfrac{3}{4}\pi {r^2}$ will be lost in $\dfrac{1}{4} \times 20\min $
$ \Rightarrow \dfrac{3}{{16}}\pi {r^2}$of the area will be reduced in $5\min $
Thus, time ${t_2}$ will be $5\min $

Note: Try to follow the solution step by step. Understand the question properly using the diagram before beginning with the solution. Alternative approaches to this problem are by finding the change in the area then applying the unitary method in the area reduction and time.