Question

In a class of 60 students, 40 students like maths, 36 students like science, 24 like both the subjects. Find the number of students who like;
i) Only maths
ii) Only science
iii) Either maths or science
iv) Neither maths nor science

Answer 1

Hint: In order to solve this question, we will first draw the Venn diagram for the same. Then we will use the Venn diagram to find the answers. Also, we have to remember that $n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)$.

Complete step-by-step solution -
In this question, we have been given that out of 60 students, 40 students like maths, 36 students like science, 24 like both the subjects, and we have been asked to find out a few values. First, we will draw the Venn diagram according to the given conditions. The Venn diagram is as below,

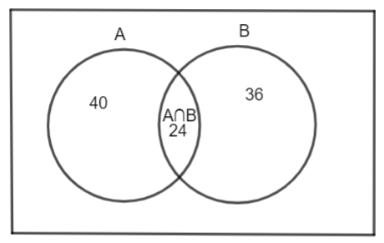
In this diagram, A represents the students who like maths whereas B represents the students who like science, and $A\cap B$ represents the students who like both. So, we can say that, $n\left( A \right)=40,n\left( B \right)=36,n\left( A\cap B \right)=24$. Now, we will find out the value for each of the given conditions.

i) The number of students who like only maths.
We will consider the number of students who like only maths as n (only maths). So, we can calculate it as,
n (only maths) $=n\left( A \right)-n\left( A\cap B \right)$
By substituting the values, we get,
n (only maths) = 40 - 24 = 16.
Hence, we can say there are 16 students who like only maths.

ii) The number of students who like only science.
We will consider the number of students who like only science as n (only science). So, we can calculate it as,
n (only science) $=n\left( B \right)-n\left( A\cap B \right)$
By substituting the values, we get,
n (only science) = 36 - 24 = 12.
Hence, we can say there are 12 students who like only science.

iii) The number of students who like either maths or science.
We will consider the number of students who like either maths or science as n (either maths or science). So, we can calculate it as,
n (either maths or science) = n (only maths) + n (only science) + n (both science and maths)
By substituting the values, we get,
n (only science) = 16 + 12 + 24 = 52
Hence, we can say there are 52 students who like either maths or science.

iv) The number of students who like neither maths nor science.
We will consider the number of students who like neither maths nor science as n (neither maths nor science). So, we can calculate it as,
n (neither maths nor science) = $60-n\left( A\cup B \right)$
Now, to calculate the value of $n\left( A\cup B \right)$, we will use the formula, $n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)$. So, putting the value in the formula, we get,
$\begin{align}
  & n\left( A\cup B \right)=40+36-24 \\
 & \Rightarrow n\left( A\cup B \right)=52 \\
\end{align}$
So, by using the value of $n\left( A\cup B \right)$, we get,
n (neither maths nor science) = 60 - 52 = 8
Hence, we can say there are 8 students who like neither maths nor science.

Note: While solving part four of this question, one can put n (only maths) as n (A), which is wrong and it will definitely give an incorrect answer. Also, in the third part, we have calculated the answer by using the formula, $n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)$, we must make sure that we don’t commit a mistake here by using $n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)+n\left( A\cap B \right)$ instead.