Question

In a class of 60 students, 40 opted for NCC, 30 opted for NSS and 20 opted for both NCC and NSS. If one of these students is selected at random, then the probability that the student selected has opted neither fore NCC nor for NSS is:
\[\begin{align}
  & A.\dfrac{2}{3} \\
 & B.\dfrac{1}{6} \\
 & C.\dfrac{1}{3} \\
 & D.\dfrac{5}{6} \\
\end{align}\]

Answer 1

Hint: To solve this question, first of all, we will assume variables for the set having students who opted for NCC or NSS. Let it be A and B. Then, we will calculate the number of students in A only or in B only by using \[n(A\text{ only)}=n(A)-n(A\cap B)\] where n (A) denotes the number of students in A. Similarly, we will calculate n (B only). Then, we will calculate $n(A\cup B)$ that is number of students in A or B or both by formula \[n(A\cup B)=n(\text{only }A)+n(\text{only }B)+n(A\cap B)\] Finally, we will calculate number of students neither in A nor in B, by subtracting $n(A\cup B)$ with total number of students. We will then, use the probability formula:
\[\text{Probability=}\dfrac{\text{favourable outcome}}{\text{total number of outcome}}\]

Complete step-by-step solution:
We are given that, the total number of students is 60. Let the total number of students who opted for NCC be A set then, the number of students in set A = 40, as there were 40 students who opted for NCC.
Let the total number of students who opted for NSS be B. Then, the number of students in set B is 30 as there were 30 students who opted for NSS.
Let n (A) represent the number of students in A.
We have 20 students opted for both NCC and NSS \[\Rightarrow n(A\cap B)=20\]
Where \[(A\cap B)\] represents A intersection B which contains all students opted for both NCC and NSS.
We have,
\[\begin{align}
  & n(A)=40 \\
 & n(B)=30 \\
 & n(A\cap B)=20 \\
\end{align}\]
Consider Venn diagram for above scenario:

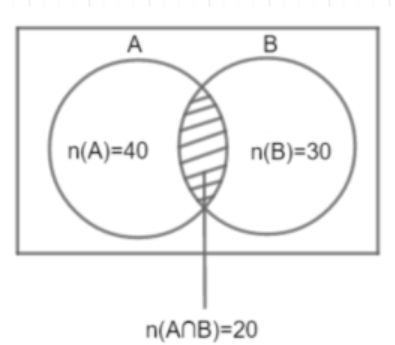
We have to calculate the probability that, the students selected have opted neither for NCC nor NSS.
Before using the probability formula, we will calculate the number of elements that are present in A only.
This can be calculated by subtracting $A\cap B$ with A.
So, \[\begin{align}
  & n(A\text{ only)}=n(A)-n(A\cap B) \\
 & \Rightarrow n(A\text{ only)}=n(A)-n(A\cap B) \\
\end{align}\]
Substituting the values of n (A) and $n\left( A\cap B \right)$ we have
\[n(\text{only }A)=40-20=20\]
Similarly, the value of \[\begin{align}
  & \text{n}\left( \text{only B} \right)=n(B)-n(A\cap B) \\
 & \Rightarrow 30-20=10 \\
\end{align}\]
So, we have

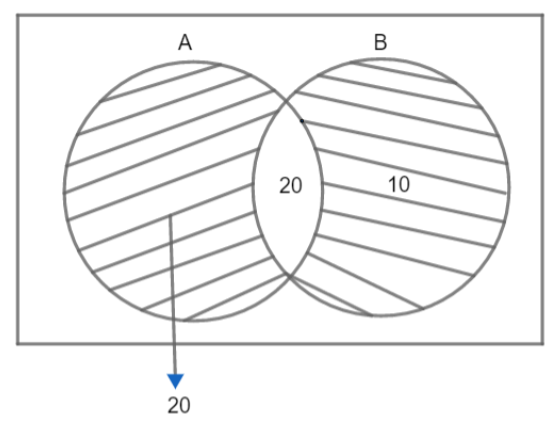
Also,
\[\begin{align}
  & \text{n(A}\cup \text{B)=total number of students in A and B} \\
 & n(A\cup B)=n(\text{only }A)+n(\text{only }B)+n(A\cap B) \\
 & n(A\cup B)=20+10+20 \\
 & n(A\cup B)=50 \\
\end{align}\]
This is obtained by using n (only A) = 20 and n (only B) = 10 as obtained above.
This is the value of the number of students who are either in A or in B or in both.
Now, finally we will calculate total number of students which are neither in NCC nor in NSS. This can be calculated by subtracting total number of students from $n(A\cup B)$
\[\text{n}\left( \text{neither NCC nor NSS} \right)\text{ }=\text{ 6}0-\text{5}0\text{ }=\text{ 1}0\]
So, number of students which are neither in NCC nor in NSS is 10.
Now, probability of an event is given as
\[\text{Probability=}\dfrac{\text{favourable outcome}}{\text{total number of outcome}}\]
Probability of students opted neither in NCC nor in NSS:
\[\Rightarrow \dfrac{\text{number of students neither in NCC nor NSS}}{\text{total number of students}}\]
Substituting value obtained in above we get:
Probability of students opted neither in NCC nor NSS \[\Rightarrow \dfrac{10}{60}=\dfrac{1}{6}\]
Therefore, the probability is $\dfrac{1}{6}$ which is option C.

Note: Another method to calculate the number of students in A or B or in both is by using formula $n(A\cup B)$ which is given as:
\[n(A\cup B)=n(A)+n(B)-n(A\cap B)\]
Substituting value of $n(A),n(B),n(A\cap B)$ we get
\[n(A\cup B)=40+30-20=70-20=50\]
So, we get $n(A\cup B)=50$. Method may differ but the value obtained is same.