Question

In a class of 50 students 35 opted for Mathematics and 37 opted for Biology. How many have opted only for Mathematics? (Assume that each student opts for at least one of the subjects).

Answer 1

Hint: In this problem, we will firstly suppose sets for students who opted for Mathematics & those who opted for Biology then apply the formula,
$n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)$
& then to find the number of students who only opted of mathematics we will apply this formula, $ = n\left( M \right) - n\left( {M \cap B} \right)$

Complete step by step solution:
Given:

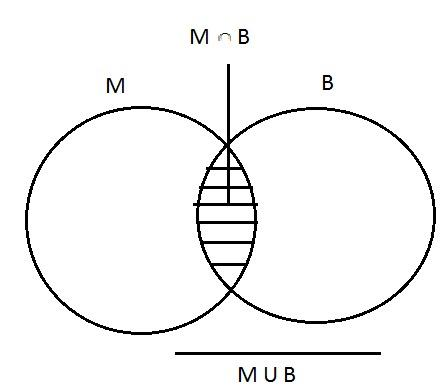
There are a total of 50 students in a class.
35 opted for Mathematics & 37 opted for Biology.
each student opts for at least one of the subjects.
To find this, let us suppose M & B be the sets for students who opted for Mathematics & Biology respectively.
According to question , we know \[\;n\left( M \right) = 35\] & $n\left( B \right) = 37$ where $n\left( M \right)$ & $n\left( B \right)$represents no. of students opted for Mathematics & Biology respectively.
$n\left( {M \cup B} \right) = 50$ where $n\left( {M \cup B} \right)$ represents total no. of students where each student opted for either of the subjects.
$n\left( {M \cap B} \right)$ represents no. of students who opted for both subjects
Now using the formula, $n\left( {M \cap B} \right) = n\left( M \right) + n\left( B \right) - n\left( {M \cup B} \right)$
= $35 + 37 - 50= 72 - 50 = 22$
\[\Rightarrow n\left( {M \cap B} \right) = 22\]
No. of students opted only for Mathematics
= no. of students opted for Mathematics – no. of students opted for both
$ = n\left( M \right) - n\left( {M \cap B} \right)$
$ = 35 - 22 = 13$

$\therefore$ The no. of students opted only for Mathematics is 13.

Note:
We need to have the concept of the Venn diagram & Sets to solve this problem. Read the question very carefully because this will help you to visualize the given conditions in your mind & will strike the way to be followed to solve the problem. Do the calculations very carefully to avoid mistake instead of knowing the concepts & procedures required