Question

In a circular motion of a particle the tangential acceleration of the particle is given by $ at = 9m{s^{ - 2}} $ . Where ‘t’ is the time. The radius of the circle described is $ 4m $ . The particle is initially at rest. Time after which total acceleration of the particle makes $ 45^\circ $ with radial acceleration is:
 $ \left( A \right)1\sec $
 $ \left( B \right)2\sec $
 $ \left( C \right)\dfrac{2}{3}\sec $
 $ \left( D \right)4\sec $

Answer 1

Hint: First draw a diagram according to the statement given in the problem where a circle of radius is there and a particle is moving, having some tangential acceleration. As the total acceleration is making an angle of $ 45^\circ $ with radial acceleration, we find the relation between the radial acceleration and tangential acceleration. Then with the help of radial acceleration formula and tangential acceleration formula we can find the time taken.

Complete step by step solution:
As per the given problem there is a circular motion of a particle where the tangential acceleration of the particle is given by $ at = 9m{s^{ - 2}} $ . The radius of the circle described is $ 4m $ . The particle is initially at rest.
Now we need to calculate the total acceleration of the particle which makes $ 45^\circ $ with radial acceleration.

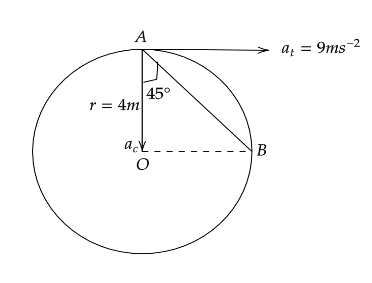
As in the diagram
AB is the total acceleration of the particle.
 $ at $ is the tangential acceleration of the particle.
 $ ac $ is the radial acceleration or we can say the centripetal acceleration of the particle.
 $ \angle OAB $ is the angle between the total acceleration and radial acceleration.
As we can see the tangential acceleration is parallel to OB hence we can say that,
OB is equal to $ at $ .
Now using in $ \vartriangle OAB $
 $ \tan \angle OAB = \dfrac{{at}}{{ac}} $
 $ \tan 45^\circ = \dfrac{{at}}{{ac}} $
We know $ \tan 45^\circ = 1 $ ,
Now we will get,
 $ 1 = \dfrac{{at}}{{ac}} $
 $ \Rightarrow at = ac \ldots \ldots \left( 1 \right) $
We can write,
 $ at = \dfrac{{dv}}{{dt}} \Rightarrow \int\limits_0^v {dv} = \int\limits_0^t {atdt} $
We know the value of $ at = 9m{s^{ - 2}} $
Now on integrating we will get,
 $ v = \int\limits_0^t {9dt} = 9t\,m{s^{ - 1}} $
We know radial acceleration is represented as,
 $ ac = \dfrac{{{v^2}}}{r} $
Where,
Velocity of the particle is v.
Radius of the circle is r.
Now from equation $ \left( 1 \right) $ we will get,
 $ at = ac $
Putting the know value we will get,
 $ 9 = \dfrac{{{v^2}}}{r} $
Now we know, $ v = 9t\,m{s^{ - 1}} $ and $ r = 4m $
 $ 9 = \dfrac{{{{\left( {9t} \right)}^2}}}{4} $
 $ \Rightarrow 9 = \dfrac{{81{t^2}}}{4} $
Cancelling the common terms we will get,
 $ 1 = \dfrac{{9{t^2}}}{4} $
Rearranging the above equation and on further solving we will get,
 $ {t^2} = \dfrac{4}{9} $
Hence the time taken is equal to $ \dfrac{2}{3}\sec $ .
Therefore the correct option is $ \left( C \right) $ .

Note:
Remember that in the rotational motion of objects tangential acceleration is measured by how quickly a tangential velocity of the moving object changes and it will work in the direction of a tangent at the point of motion. And also due this tangential change in the direction centripetal acceleration also comes into play.