Question

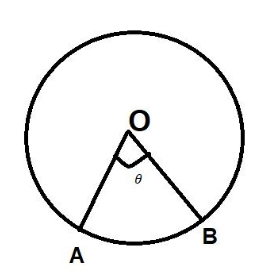
In a circle of radius 21 cm, an arc subtends an angle of ${60^0}$at the center. Find the length of the arc and area of the sector formed by the arc. (Use$\pi = \dfrac{{22}}{7}$)

Answer 1

Hint: Here we use the formula of length of arc i.e. $\dfrac{\theta }{{{{360}^0}}} \times 2\pi r$ and area of the sector i.e. $\dfrac{\theta }{{{{360}^0}}} \times \pi {r^2}$. just put the value of radius and angle to get the answer.

Complete step-by-step answer:

Given radius of circle, r =21 cm
Arc subtends an angle of ${60^0}$ at center.
We know that for finding the length of arc the formula we use is $\dfrac{\theta }{{{{360}^0}}} \times 2\pi r$.
So the length of an arc AB\[ = \dfrac{\theta }{{{{360}^0}}} \times 2\pi r = \dfrac{{{{60}^0}}}{{{{360}^0}}} \times 2 \times \dfrac{{22}}{7} \times 21 = \dfrac{1}{6} \times 2 \times 22 \times 3 = 22cm\]
And for the area of sector the formula we use is$\dfrac{\theta }{{{{360}^0}}} \times \pi {r^2}$.
So the area of sector OAB$ = \dfrac{\theta }{{{{360}^0}}} \times \pi {r^2} = \dfrac{{60}}{{360}} \times \dfrac{{22}}{7} \times {(22)^2} = 11 \times 3 \times 7 = 231c{m^2}$
Therefore the length of arc is 22cm and the area of the sector is $231c{m^2}$

Note: Whenever we face such a type of question we simply use the formula to get the answer. And if you forgot the formula you can apply a unitary method for solving the question. As you know the total angle at the center of the circle is ${360^0}$. And for the complete angle, we know that the total length of the arc of the circle is$ 2\pi r$ also known as circumference of circle. Then for angle $\theta $ we can simply apply a unitary method. Similarly we can also find the area of the sector.