Question

Imagine yourself in a rain steadily falling vertically with a speed of $2 m/s$.
(a) If you start moving with $1 m/s$ due east, in which direction should you hold the umbrella to protect yourself from the rain?
(b) On a sunny day, at 12 noon, you hold an umbrella vertically. If you run at a certain speed, do you need to incline the umbrella? Justify your answer.

Answer 1

Hint: Due to relative motion between rain and man, the rain will not fall vertically on the running person. Calculate the angle made by the velocity of the rain with respect to the velocity of man using vector representation. The angle must be the angle between velocity of the rain with respect to man and the vertical upward direction. For the second part, assume the velocity of the sunlight has the speed of light.

Complete step by step answer:
(a) Let’s denote the speed of rain as \[{v_r}\] and speed of the man as \[{v_m}\]. If we start running by holding the umbrella vertically, due to relative motion of the rain, we will get wet. Now, let’s express the motion of the rain and the man using vectors as follows,

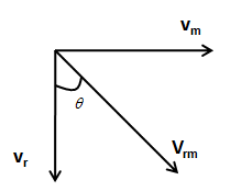
In the above figure, \[{v_{rm}}\] is the velocity of the rain with respect to the man and \[\theta \] is the angle made by \[{v_{rm}}\] with the vertical. If the direction of \[{v_{rm}}\] is along –z-axis then the man has to hold the umbrella along the +z-axis to protect himself from the rain.

Let’s calculate the angle \[\theta \] from the geometry of the above figure as follows,
\[\tan \theta = \dfrac{{{v_m}}}{{{v_r}}}\]
Substituting 2 m/s for \[{v_r}\] and 1 m/s for \[{v_m}\] in the above equation, we get,
\[\tan \theta = \dfrac{1}{2}\]
\[ \Rightarrow \theta = {\tan ^{ - 1}}\left( {0.5} \right)\]
\[ \Rightarrow \theta = 26.7^\circ \]

Thus, we should hold the umbrella as shown in the figure below.

Therefore, we should hold the umbrella towards the west at an angle \[26.7^\circ \] from the vertical.

(b) We know that the velocity of sunlight is \[3 \times {10^8}\,{\text{m/s}}\] which is very greater than our speed. Therefore, let’s express the angle made by the velocity of sunlight with respect to our velocity as follows,
\[\tan \theta = \dfrac{{{v_m}}}{{{v_s}}}\]
Here, \[{v_m}\] is the velocity of man and \[{v_s}\] is the velocity of sunlight.

Since, \[{v_s} > > {v_m}\] , we get,
\[\tan \theta = 0\]
\[ \Rightarrow \theta = {\tan ^{ - 1}}\left( 0 \right)\]
\[ \therefore \theta = 0^\circ \]

Therefore, the angle is \[0^\circ \]. Thus, we don’t need to incline the umbrella.

Note: Do not calculate the angle made by the velocity of the rain with respect to man and the velocity of the man. Always do calculate the angle between velocity of the rain with respect to man and the vertical upward direction. If you run with speed compared to the speed of light, then you have to incline the umbrella but this is almost impossible.