Question

If ${{z}_{1}},{{z}_{2}},{{z}_{3}}\And {{z}_{4}}$ be the vertices of a square in Argand plane, then:
(a)$2{{z}_{2}}=\left( 1-i \right){{z}_{1}}+\left( 1+i \right){{z}_{3}}$
(b) $2{{z}_{2}}=\left( 2-i \right){{z}_{1}}+\left( 2+i \right){{z}_{3}}$
(c) $2{{z}_{2}}=\left( 3-i \right){{z}_{1}}+\left( 3+i \right){{z}_{3}}$
(d) $2{{z}_{2}}=\left( 4-i \right){{z}_{1}}+\left( 4+i \right){{z}_{3}}$

Answer 1

Hint: First of all draw a square with vertices as ${{z}_{1}},{{z}_{2}},{{z}_{3}}\And {{z}_{4}}$. Then we know that the angle between two adjacent sides of the square is ${{90}^{\circ }}$. Then we can apply anti clockwise rotation between the vectors $\left( {{z}_{3}}-{{z}_{2}} \right)\And \left( {{z}_{1}}-{{z}_{2}} \right)$. These vectors are adjacent to each other so the angle of rotation is ${{90}^{\circ }}$. If two complex numbers ${{z}_{5}},{{z}_{6}}$ then the rotation of these complex numbers is done as follows ${{z}_{6}}=\dfrac{\left| {{z}_{6}} \right|}{\left| {{z}_{5}} \right|}{{e}^{i\theta }}$. Here, ${{z}_{6}}$ is the vector after rotation and angle of rotation is $\theta $. This is how we are going to apply the rotation. Then simplify it to get the result in the form of one of the options given.

Complete step-by-step solution:
We have given 4 vertices of a square in Argand plane as follows:
${{z}_{1}},{{z}_{2}},{{z}_{3}}\And {{z}_{4}}$
In the below figure, we have drawn a square with vertices as ${{z}_{1}},{{z}_{2}},{{z}_{3}}\And {{z}_{4}}$ we get,

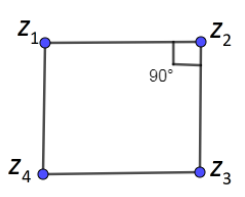
Now, we are going to apply rotation between the complex vectors $\left( {{z}_{3}}-{{z}_{2}} \right)\And \left( {{z}_{1}}-{{z}_{2}} \right)$ and the angle of rotation is ${{90}^{\circ }}$ because these vectors are adjacent sides of the square and from the figure, you can see that angle between adjacent sides of the square is ${{90}^{\circ }}$. We know that rotation should be anti clockwise so when we apply rotation in anticlockwise sense then the final vector is $\left( {{z}_{3}}-{{z}_{2}} \right)$ and the initial vector is $\left( {{z}_{1}}-{{z}_{2}} \right)$.
In the below diagram, we have shown ${{z}_{5}},{{z}_{6}}\And {{z}_{7}}$ are the three vertices which are forming an angle $\theta $ in the following way:

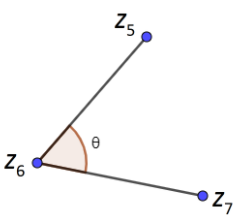
Now, applying anti clockwise rotation on the above complex numbers we get,
${{z}_{5}}-{{z}_{6}}=\dfrac{\left| {{z}_{5}}-{{z}_{6}} \right|}{\left| {{z}_{7}}-{{z}_{6}} \right|}{{e}^{i\theta }}$
In the above equation, $\left| {{z}_{5}}-{{z}_{6}} \right|\And \left| {{z}_{7}}-{{z}_{6}} \right|$ are the magnitudes of the vectors $\left( {{z}_{5}}-{{z}_{6}} \right)\And \left( {{z}_{7}}-{{z}_{6}} \right)$ and angle of rotation $\theta $.
$\left( {{z}_{3}}-{{z}_{2}} \right)=\dfrac{\left| {{z}_{3}}-{{z}_{2}} \right|}{\left| {{z}_{1}}-{{z}_{2}} \right|}\left( {{z}_{1}}-{{z}_{2}} \right){{e}^{i\dfrac{\pi }{2}}}$
We know that:
${{e}^{i\dfrac{\pi }{2}}}=\cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2}$
Using the above relation in the above complex vector equation we get,
$\left( {{z}_{3}}-{{z}_{2}} \right)=\dfrac{\left| {{z}_{3}}-{{z}_{2}} \right|}{\left| {{z}_{1}}-{{z}_{2}} \right|}\left( {{z}_{1}}-{{z}_{2}} \right)\left( \cos \dfrac{\pi }{2}+i\sin \dfrac{\pi }{2} \right)$
As $\left| {{z}_{3}}-{{z}_{2}} \right|\And \left| {{z}_{1}}-{{z}_{2}} \right|$ are the magnitude of the vectors which are the sides of the square and we know that all the sides of the square are equal so both these magnitudes are equal and the ratio of both these magnitudes is 1.
$\dfrac{\left| {{z}_{3}}-{{z}_{2}} \right|}{\left| {{z}_{1}}-{{z}_{2}} \right|}=1$
We also know that the value of following trigonometric ratios that are used in the above complex vector equation:
$\begin{align}
  & \cos \dfrac{\pi }{2}=0, \\
 & \sin \dfrac{\pi }{2}=1 \\
\end{align}$
Using the above value of trigonometric ratios and the ratio of the magnitudes in the complex vector eq. we get,
$\begin{align}
  & \left( {{z}_{3}}-{{z}_{2}} \right)=\left( {{z}_{1}}-{{z}_{2}} \right)\left( 0+i\left( 1 \right) \right) \\
 & \Rightarrow \left( {{z}_{3}}-{{z}_{2}} \right)=\left( {{z}_{1}}-{{z}_{2}} \right)i \\
\end{align}$
Rearranging the above equation we get,
${{z}_{3}}-{{z}_{1}}i={{z}_{2}}\left( 1-i \right)$
Dividing both the sides by $1-i$ in the above equation we get,
$\dfrac{{{z}_{3}}-{{z}_{1}}i}{\left( 1-i \right)}={{z}_{2}}$
Rationalizing the left hand side of the above by multiplying and dividing by $1+i$ we get,
\[\begin{align}
  & \dfrac{{{z}_{3}}-{{z}_{1}}i}{\left( 1-i \right)}\times \left( \dfrac{1+i}{1+i} \right)={{z}_{2}} \\
 & \Rightarrow \dfrac{{{z}_{3}}\left( 1+i \right)-{{z}_{1}}i\left( 1+i \right)}{\left( 1-i \right)\left( 1+i \right)}={{z}_{2}} \\
 & \Rightarrow \dfrac{{{z}_{3}}\left( 1+i \right)-{{z}_{1}}\left( i+{{i}^{2}} \right)}{\left( 1-{{i}^{2}} \right)}={{z}_{2}} \\
\end{align}\]
In the complex number, we know that the square of iota is -1.
${{i}^{2}}=-1$
Substituting the above value of square of iota in the above complex number equation we get,
\[\begin{align}
  & \dfrac{{{z}_{3}}\left( 1+i \right)-{{z}_{1}}\left( i-1 \right)}{\left( 1-\left( -1 \right) \right)}={{z}_{2}} \\
 & \Rightarrow \dfrac{{{z}_{3}}\left( 1+i \right)+{{z}_{1}}\left( -i+1 \right)}{\left( 2 \right)}={{z}_{2}} \\
 & \Rightarrow {{z}_{3}}\left( 1+i \right)+{{z}_{1}}\left( -i+1 \right)=2{{z}_{2}} \\
\end{align}\]
Now, comparing the above value of the relation with the options given in the above problem we get the correct option as (a).

Note: In the above problem, you have applied the rotation on the vectors made from the complex numbers in the following manner:
${{z}_{5}}-{{z}_{6}}=\dfrac{\left| {{z}_{5}}-{{z}_{6}} \right|}{\left| {{z}_{7}}-{{z}_{6}} \right|}\left( {{z}_{7}}-{{z}_{6}} \right){{e}^{i\theta }}$
Now, as you can see that we have given a square meaning all the sides are equal so the magnitude of the two vectors $\left( {{z}_{5}}-{{z}_{6}} \right)\And \left( {{z}_{7}}-{{z}_{6}} \right)$ are equal and their ratio is one. The catch is that, it is not always necessary that the magnitudes of the vectors are equal but generally students forget the magnitude of the vectors and write the above rotation expression as:
${{z}_{5}}-{{z}_{6}}=\left( {{z}_{7}}-{{z}_{6}} \right){{e}^{i\theta }}$
So, don’t make this mistake and always remember the formula in the following way:
${{z}_{5}}-{{z}_{6}}=\dfrac{\left| {{z}_{5}}-{{z}_{6}} \right|}{\left| {{z}_{7}}-{{z}_{6}} \right|}\left( {{z}_{7}}-{{z}_{6}} \right){{e}^{i\theta }}$