Question

If $ y=x $ is a tangent to the parabola $ y=a{{x}^{2}}+c $ and $ a=2 $ , then find the value of $ c $ .
(a) 1
(b) $ -\dfrac{1}{2} $
(c) $ \dfrac{1}{2} $
(d) $ \dfrac{1}{8} $

Answer 1

Hint: In this question, first draw the diagram or the graph according to the conditions mentioned in the question. Find the slope of the tangent and the parabola by differentiating with respect to $ x $ and equate them to find the value of the $ x $ . Substitute the value of $ x $ in the equation of parabola and get the point of contact $ \left( x,\,y \right) $ . Finally, use the equation of tangent and the point of contact to find the value of $ c $ .

Complete step by step answer:
 $ \Rightarrow $ Here, we have the equation of tangent $ y=x $ and the equation of parabola $ y=a{{x}^{2}}+c $ , let us draw the diagram representing the values and conditions it is given in the question.

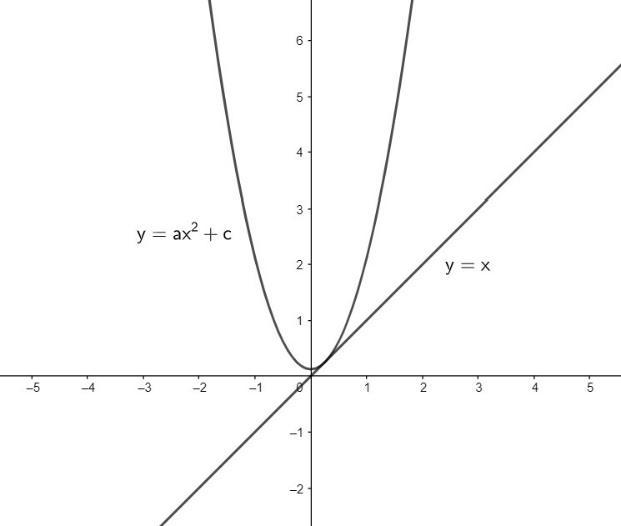
 $ \Rightarrow $ Let us first differentiate the equation of tangent with respect to $ x $ , we get
 $ \dfrac{dy}{dx}=1 $
 $ \Rightarrow $ Since, the $ y=x $ is a tangent of the parabola, the slope of the parabola is equal to the slope of the tangent. Therefore,
 $ \begin{align}
  & \dfrac{dy}{dx}=a\left( 2x \right)+0 \\
 & =2ax
\end{align} $
Since, value of $ a=2 $ ,
 $ \begin{align}
  & \dfrac{dy}{dx}=2\left( 2 \right)x \\
 & =4x
\end{align} $
 $ \Rightarrow $ We know, $ m=\dfrac{dy}{dx} $
 $ 1=4x $
 $ \dfrac{1}{4}=x $
 $ \Rightarrow $ Now, let us substitute the value of $ x $ in the equation of the parabola, we get
 $ y=2{{\left( \dfrac{1}{4} \right)}^{2}}+c $
     $ \begin{align}
  & =2\left( \dfrac{1}{16} \right)+c \\
 & =\dfrac{1}{8}+c
\end{align} $
 $ \Rightarrow $ Therefore, the point of contact $ \left( x,\,y \right)=\left( \dfrac{1}{4},\,\dfrac{1}{8}+c \right) $ .
 $ \Rightarrow $ We also know, that from the equation of tangent we have $ y=x $ .
 $ \Rightarrow $ Now, from the point of contact, we can say that $ \dfrac{1}{8}+c=\dfrac{1}{4} $
 $ \Rightarrow $ Simplify the above expression, to find the value of $ c $ .
 $ \Rightarrow $ First, let us subtract by $ -\dfrac{1}{8} $ on both the sides of the equation, we get
 $ \dfrac{1}{8}+c-\dfrac{1}{8}=\dfrac{1}{4}-\dfrac{1}{8} $
   $ \Rightarrow $ $ c=\dfrac{1}{4}-\dfrac{1}{8} $
 $ \Rightarrow $ Let us equalize the denominator, by multiplying and dividing by 2 in the numerator and denominator of the fraction $ \dfrac{1}{4} $ , we get
 $ \begin{align}
  & c=\dfrac{1\times 2}{4\times 2}-\dfrac{1}{8} \\
 & =\dfrac{2}{8}-\dfrac{1}{8} \\
 & =\dfrac{2-1}{8} \\
 & =\dfrac{1}{8}
\end{align} $
 $ \Rightarrow $ Hence, the value of c is $ \dfrac{1}{8} $ .

Note:
 This question can also be solved by another method. First, arrange the equation of parabola in the form of $ {{\left( x-h \right)}^{2}}=4A\left( y-k \right) $ , the value of $ h=0 $ , $ A=\dfrac{1}{4a} $ , $ k=c $ . From the equation of tangent, we will get the slope $ m=1 $ and the value of the constant $ C=0 $ . Now, by using the condition of tangency, $ C=-mh+k-A{{m}^{2}} $ , we can find the value of $ c $ .