Question

If we have the vertices as $O\left( 0,0 \right),A\left( 1,2 \right),B\left( 3,4 \right)$ of $\Delta OAB$ . The joint equation of the altitude and median drawn from $O$ is.
(a) ${{x}^{2}}+7xy-{{y}^{2}}=0$
(b) ${{x}^{2}}+7xy+{{y}^{2}}=0$
(c) $3{{x}^{2}}-xy-2{{y}^{2}}=0$
(d) $3{{x}^{2}}+xy-2{{y}^{2}}=0$

Answer 1

Hint: For solving this question first we will find the coordinates of the midpoint of the side AB with the help of the formula $C\equiv \left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ and slope of the side AB with the help of the formula ${{m}_{AB}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ . After that, we will find the equation of median from the formula ${{L}_{AB}}:\left( y-{{y}_{1}} \right)=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}\left( x-{{x}_{1}} \right)$ and find the slope of the altitude and its equation by the formula $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$ . Then, we will find the combined equation of altitude and median from the formula ${{L}_{1}}\times {{L}_{2}}=0$ easily.

Complete step-by-step solution -
Given:
It is given that $O\left( 0,0 \right),A\left( 1,2 \right),B\left( 3,4 \right)$ are the vertices of $\Delta OAB$ and we have to find the joint equation of the altitude and median drawn from point $O$ to the side AB.
Now, we will use the following formulas of coordinate geometry to solve this question:
1. If $A\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ and $B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ then, coordinates of the midpoint of segment AB will be $C\equiv \left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ .
2. The slope of line AB through points $A\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ and $B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ is ${{m}_{AB}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ and the equation of line AB will be ${{L}_{AB}}:\left( y-{{y}_{1}} \right)=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}\left( x-{{x}_{1}} \right)$ or $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$
3. If two lines are perpendicular then the product of their slopes will be equal to -1.
4. If ${{L}_{1}}=0$ and ${{L}_{2}}=0$ are two distinct lines then their joint equation will be ${{L}_{1}}\times {{L}_{2}}=0$ .
Now, we will find the equation of median and the altitude first and then we will find their joint equation.
Equation of median from point O on the side AB:
Now, let C be the midpoint of the $A\equiv \left( 1,2 \right)$ and $B\equiv \left( 3,4 \right)$so, using the midpoint formula to write the coordinates of C. Then,
$\begin{align}
  & C\equiv \left( \dfrac{1+3}{2},\dfrac{2+4}{2} \right) \\
 & \Rightarrow C\equiv \left( 2,3 \right) \\
\end{align}$
Now, median on the side AB will be passing thorough points $O\equiv \left( 0,0 \right)$ and $C\equiv \left( 2,3 \right)$ then using the formula ${{L}_{OC}}:\left( y-{{y}_{1}} \right)=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}\left( x-{{x}_{1}} \right)$ to write it’s equation. Then,
$\begin{align}
  & {{L}_{OC}}:\left( y-{{y}_{1}} \right)=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}\left( x-{{x}_{1}} \right) \\
 & \Rightarrow {{L}_{OC}}:\left( y-0 \right)=\dfrac{\left( 3-0 \right)}{\left( 2-0 \right)}\left( x-0 \right) \\
 & \Rightarrow {{L}_{OC}}:y=\dfrac{3}{2}x \\
 & \Rightarrow {{L}_{OC}}:2y=3x \\
 & \Rightarrow {{L}_{OC}}:3x-2y=0 \\
\end{align}$
Now, from the above result, we conclude that the equation of the median from point O on the side AB will be ${{L}_{Median}}:3x-2y=0$ .
Equation of altitude from point O on the side AB:
Now, it is given that $A\equiv \left( 1,2 \right)$ and $B\equiv \left( 3,4 \right)$ then, the slope of the line through points A and B will be ${{m}_{AB}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\dfrac{4-2}{3-1}=\dfrac{2}{2}=1$ . And altitude from point O will be perpendicular to the side AB so, the slope of the altitude will be $-1$ .
Now, altitude on the side AB will be passing through points $O\equiv \left( 0,0 \right)$ and having slope $-1$ then using the formula $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$ to write it’s equation. Then,
$\begin{align}
  & \left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right) \\
 & \Rightarrow y=-x \\
 & \Rightarrow x+y=0 \\
\end{align}$
Now, from the above result we conclude that the equation of the altitude through point O on the side AB will be ${{L}_{Altitude}}:x+y=0$ .
Now, the combined equation of the altitude and median from the point O will be ${{L}_{Median}}\times {{L}_{Altitude}}$ . Then,
$\begin{align}
  & {{L}_{Median}}\times {{L}_{Altitude}}=\left( 3x-2y \right)\left( x+y \right)=0 \\
 & \Rightarrow {{L}_{Median}}\times {{L}_{Altitude}}=3{{x}^{2}}+3xy-2xy-2{{y}^{2}}=0 \\
 & \Rightarrow {{L}_{Median}}\times {{L}_{Altitude}}=3{{x}^{2}}+xy-2{{y}^{2}}=0 \\
\end{align}$
Now, from the above result, we conclude that the combined equation of the altitude and median from point O will be $3{{x}^{2}}+xy-2{{y}^{2}}=0$ . For more clarity look at the figure given below:

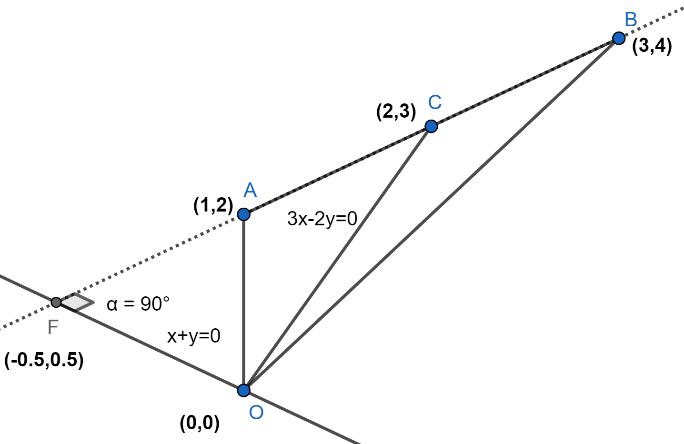
In the above figure OF is the altitude on the side, AB and OC is the median on the side AB.
Hence, (d) is the correct option.

Note: Here, the student must proceed stepwise in the solution and proceed in the right direction to get the correct answer quickly. After that, we should solve stepwise and proceed as per the data given in the question. Moreover, we should use each formula with the correct values and take care of signs as well. Then, avoid calculation mistakes while solving to get the correct answer.