Question

If U is the universal set and $A\subset U$ then fill in the blanks:
(a). $A\cup A'=........$
(b). $A\cap A'=.........$
(c). $\phi '\cap A=........$
(d). $U'\cap A=........$

Answer 1

Hint: First we will use the Venn diagram and we will solve this question by first understanding the meaning of complement of a set, and then what is union and intersection of sets and then we will find the value of all the options.

Complete step-by-step answer:

Let’s first write the definition of some terms,
Universal set: The set containing all objects or elements and of which all other sets are subsets.
Complement of a set: Complement of a set A, denoted by A c, is the set of all elements that belongs to the universal set but does not belong to set A.
Union: The union (denoted by $\cup $ ) of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations through which sets can be combined and related to each other.
Intersection: The intersection of two sets has only the elements common to both sets. If an element is in just one set it is not part of the intersection. The symbol is an upside down $\cap $ .

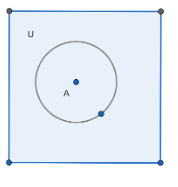
Let’s start solving each part one by one.
For (a):
$A\cup A'$ covers the whole universal set by the given diagram and definition it is clear.
Hence, $A\cup A'$ = U.
Now we will solve part (b):
Now $A\cap A'$ will be null set by the definition of intersection and complement of the set and from the Venn diagram also we can see that.
Hence,
$A\cap A'=\phi $
Let’s solve part (c):
Now $\phi '$ will be a universal set U.
Now from the given diagram we can see that,
$\phi '\cap A$ will be equal to A.
Hence, $\phi '\cap A$ = A.
For part (d):
Now $U'$ will be null set $\phi $ .
Now from the given diagram we can see that,
$U'\cap A$ will be equal to $\phi $.
Hence, $U'\cap A$= $\phi $.
Hence, we have found all the values.

Note: One can also solve this question by taking some values of the set U and A, and then can find all the values of the given option easily. The definition that we have used should be kept in mind.