
If two vertices of an equilateral triangle are \[\left( 0,0 \right)\] and \[\left( 0,2\sqrt{3} \right)\] then find the third vertex of the equilateral triangle.
Answer
565.8k+ views
Hint: We solve this problem by using the slopes and angle between lines.
We have the condition that all the angles in an equilateral triangle are equal to \[{{60}^{\circ }}\]
We assume that the coordinates of the required third vertex as some variables then we find the slopes of required lines.
We have the formula of slope of two points \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\] is given as
\[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]
We also have the formula that if \[\theta \]is the angle between two having the slopes \[{{m}_{1}},{{m}_{2}}\] then,
\[\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|\]
We use the condition that if a line having slope \[m\]makes an angle \[\theta \] with positive X – axis in anti – clockwise direction then
\[m=\tan \theta \]
Complete step by step answer:
We are given that the two vertices of an equilateral triangle are \[\left( 0,0 \right)\] and \[\left( 0,2\sqrt{3} \right)\]
Let us assume that the given two vertices as \[A\left( 0,0 \right)\] and \[B\left( 0,2\sqrt{3} \right)\] of triangle \[\Delta ABC\]
Let us assume that the required third vertex as \[C\left( h,k \right)\]
Now, let us take a rough figure that represents the given equilateral triangle as
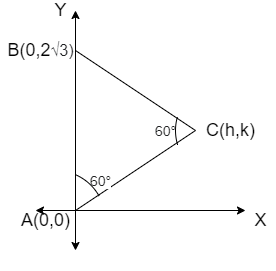
Now, let us find the slope of line AC
We know that the formula of slope of two points \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\] is given as
\[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]
By using the above formula to vertices A and C then we get the slope of AC as
\[\begin{align}
& \Rightarrow {{m}_{AC}}=\dfrac{k-0}{h-0} \\
& \Rightarrow {{m}_{AC}}=\dfrac{k}{h} \\
\end{align}\]
We know that all the angles in an equilateral triangle are equal to \[{{60}^{\circ }}\]
By using the above statement we get
\[\Rightarrow \angle CAB=\angle ACB={{60}^{\circ }}\]
We know that the axes are perpendicular to each other
By using the above condition to X – axis and Y – axis then we get
\[\begin{align}
& \Rightarrow \angle YAX={{90}^{\circ }} \\
& \Rightarrow \angle YAC+\angle CAX={{90}^{\circ }} \\
& \Rightarrow \angle CAX={{90}^{\circ }}-{{60}^{\circ }} \\
& \Rightarrow \angle CAX={{30}^{\circ }} \\
\end{align}\]
We know that the condition that if a line having slope \[m\]makes an angle \[\theta \] with positive X – axis in anti – clockwise direction then
\[m=\tan \theta \]
By using the above condition to line AC we get
\[\begin{align}
& \Rightarrow {{m}_{AC}}=\tan \left( \angle CAX \right) \\
& \Rightarrow {{m}_{AC}}=\tan \left( {{30}^{\circ }} \right) \\
\end{align}\]
We know that the standard value from trigonometric ratios that is
\[\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}\]
By substituting the required values in above equation then we get
\[\begin{align}
& \Rightarrow \dfrac{k}{h}=\dfrac{1}{\sqrt{3}} \\
& \Rightarrow h=k\sqrt{3}.........equation(i) \\
\end{align}\]
Now, let us find the slope of line BC
By using the slope formula we get the slope of line BC as
\[\begin{align}
& \Rightarrow {{m}_{BC}}=\dfrac{k-2\sqrt{3}}{h-0} \\
& \Rightarrow {{m}_{BC}}=\dfrac{k-2\sqrt{3}}{h} \\
\end{align}\]
We know that the formula that if \[\theta \]is the angle between two having the slopes \[{{m}_{1}},{{m}_{2}}\] then,
\[\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|\]
By using the above formula to lines AC and CB we get
\[\begin{align}
& \Rightarrow \tan {{60}^{\circ }}=\left| \dfrac{{{m}_{AC}}-{{m}_{BC}}}{1+{{m}_{AC}}{{m}_{BC}}} \right| \\
& \Rightarrow \sqrt{3}=\left| \dfrac{\dfrac{k}{h}-\dfrac{k-2\sqrt{3}}{h}}{1+\left( \dfrac{k}{h} \right)\left( \dfrac{k-2\sqrt{3}}{h} \right)} \right|..........equation(ii) \\
\end{align}\]
We know that if \[\left| x \right|=a\] then \[x=\pm a\]
We have the value of \[h\] from equation (i) as
\[h=k\sqrt{3}\]
By using the above conditions to equation (ii) and taking the positive sign first then we get
\[\begin{align}
& \Rightarrow \dfrac{\dfrac{k}{k\sqrt{3}}-\dfrac{k-2\sqrt{3}}{k\sqrt{3}}}{1+\dfrac{k-2\sqrt{3}}{3k}}=\sqrt{3} \\
& \Rightarrow \dfrac{k-k+2\sqrt{3}}{k\sqrt{3}}=\sqrt{3}\left( \dfrac{3k+k-2\sqrt{3}}{3k} \right) \\
& \Rightarrow 2=\dfrac{4k-2\sqrt{3}}{\sqrt{3}} \\
\end{align}\]
Now, by cross multiplying the terms in LHS and RHS then we get the value of \[k\] as
\[\begin{align}
& \Rightarrow 2\sqrt{3}=4k-2\sqrt{3} \\
& \Rightarrow 4k=4\sqrt{3} \\
& \Rightarrow k=\sqrt{3} \\
\end{align}\]
Now, by substituting the value of \[k\] in equation (i) then we get
\[\begin{align}
& \Rightarrow h=\left( \sqrt{3} \right)\sqrt{3} \\
& \Rightarrow h=3 \\
\end{align}\]
So, we can say that the third vertex is \[\left( 3,\sqrt{3} \right)\]
Now, let us take the negative sign in the equation (ii) then we get
\[\begin{align}
& \Rightarrow \dfrac{\dfrac{k}{k\sqrt{3}}-\dfrac{k-2\sqrt{3}}{k\sqrt{3}}}{1+\dfrac{k-2\sqrt{3}}{3k}}=-\sqrt{3} \\
& \Rightarrow \dfrac{k-k+2\sqrt{3}}{k\sqrt{3}}=-\sqrt{3}\left( \dfrac{3k+k-2\sqrt{3}}{3k} \right) \\
& \Rightarrow 2=-\left( \dfrac{4k-2\sqrt{3}}{\sqrt{3}} \right) \\
\end{align}\]
Now, by cross multiplying the terms in LHS and RHS then we get the value of \[k\] as
\[\begin{align}
& \Rightarrow 2\sqrt{3}=-4k+2\sqrt{3} \\
& \Rightarrow 4k=0 \\
& \Rightarrow k=0 \\
\end{align}\]
Now, by substituting the value of \[k\] in equation (i) then we get
\[\begin{align}
& \Rightarrow h=\left( 0 \right)\sqrt{3} \\
& \Rightarrow h=0 \\
\end{align}\]
Here, we can see that the vertex we get is \[\left( 0,0 \right)\] which is already given.
Therefore, we can conclude that the third vertex of the given equilateral triangle is \[\left( 3,\sqrt{3} \right)\]
Note:
We have a shortcut for solving this problem.
Let us take the rough figure of the given triangle as

Here, we can see that the value of \[h\] is the height of the triangle and \[k\] is half of side AB
Let us find the distance AB
We know that the distance formula if two points \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\] is given as
\[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
By using the above formula we get the distance AB as
\[\begin{align}
& \Rightarrow AB=\sqrt{{{\left( 2\sqrt{3}-0 \right)}^{2}}+{{\left( 0-0 \right)}^{2}}} \\
& \Rightarrow AB=2\sqrt{3} \\
\end{align}\]
Now, let us find the value of \[k\] which is half of AB
By using the above condition we get
\[\begin{align}
& \Rightarrow k=\dfrac{2\sqrt{3}}{2} \\
& \Rightarrow k=\sqrt{3} \\
\end{align}\]
We know that the height of equilateral triangle of side \[a\] is given as
\[height=\dfrac{\sqrt{3}}{2}a\]
By using the above formula we get the value of \[h\] as
\[\begin{align}
& \Rightarrow h=\dfrac{\sqrt{3}}{2}\left( 2\sqrt{3} \right) \\
& \Rightarrow h=3 \\
\end{align}\]
Therefore, we can conclude that the third vertex of the given equilateral triangle is \[\left( 3,\sqrt{3} \right)\]
We have the condition that all the angles in an equilateral triangle are equal to \[{{60}^{\circ }}\]
We assume that the coordinates of the required third vertex as some variables then we find the slopes of required lines.
We have the formula of slope of two points \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\] is given as
\[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]
We also have the formula that if \[\theta \]is the angle between two having the slopes \[{{m}_{1}},{{m}_{2}}\] then,
\[\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|\]
We use the condition that if a line having slope \[m\]makes an angle \[\theta \] with positive X – axis in anti – clockwise direction then
\[m=\tan \theta \]
Complete step by step answer:
We are given that the two vertices of an equilateral triangle are \[\left( 0,0 \right)\] and \[\left( 0,2\sqrt{3} \right)\]
Let us assume that the given two vertices as \[A\left( 0,0 \right)\] and \[B\left( 0,2\sqrt{3} \right)\] of triangle \[\Delta ABC\]
Let us assume that the required third vertex as \[C\left( h,k \right)\]
Now, let us take a rough figure that represents the given equilateral triangle as

Now, let us find the slope of line AC
We know that the formula of slope of two points \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\] is given as
\[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]
By using the above formula to vertices A and C then we get the slope of AC as
\[\begin{align}
& \Rightarrow {{m}_{AC}}=\dfrac{k-0}{h-0} \\
& \Rightarrow {{m}_{AC}}=\dfrac{k}{h} \\
\end{align}\]
We know that all the angles in an equilateral triangle are equal to \[{{60}^{\circ }}\]
By using the above statement we get
\[\Rightarrow \angle CAB=\angle ACB={{60}^{\circ }}\]
We know that the axes are perpendicular to each other
By using the above condition to X – axis and Y – axis then we get
\[\begin{align}
& \Rightarrow \angle YAX={{90}^{\circ }} \\
& \Rightarrow \angle YAC+\angle CAX={{90}^{\circ }} \\
& \Rightarrow \angle CAX={{90}^{\circ }}-{{60}^{\circ }} \\
& \Rightarrow \angle CAX={{30}^{\circ }} \\
\end{align}\]
We know that the condition that if a line having slope \[m\]makes an angle \[\theta \] with positive X – axis in anti – clockwise direction then
\[m=\tan \theta \]
By using the above condition to line AC we get
\[\begin{align}
& \Rightarrow {{m}_{AC}}=\tan \left( \angle CAX \right) \\
& \Rightarrow {{m}_{AC}}=\tan \left( {{30}^{\circ }} \right) \\
\end{align}\]
We know that the standard value from trigonometric ratios that is
\[\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}\]
By substituting the required values in above equation then we get
\[\begin{align}
& \Rightarrow \dfrac{k}{h}=\dfrac{1}{\sqrt{3}} \\
& \Rightarrow h=k\sqrt{3}.........equation(i) \\
\end{align}\]
Now, let us find the slope of line BC
By using the slope formula we get the slope of line BC as
\[\begin{align}
& \Rightarrow {{m}_{BC}}=\dfrac{k-2\sqrt{3}}{h-0} \\
& \Rightarrow {{m}_{BC}}=\dfrac{k-2\sqrt{3}}{h} \\
\end{align}\]
We know that the formula that if \[\theta \]is the angle between two having the slopes \[{{m}_{1}},{{m}_{2}}\] then,
\[\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|\]
By using the above formula to lines AC and CB we get
\[\begin{align}
& \Rightarrow \tan {{60}^{\circ }}=\left| \dfrac{{{m}_{AC}}-{{m}_{BC}}}{1+{{m}_{AC}}{{m}_{BC}}} \right| \\
& \Rightarrow \sqrt{3}=\left| \dfrac{\dfrac{k}{h}-\dfrac{k-2\sqrt{3}}{h}}{1+\left( \dfrac{k}{h} \right)\left( \dfrac{k-2\sqrt{3}}{h} \right)} \right|..........equation(ii) \\
\end{align}\]
We know that if \[\left| x \right|=a\] then \[x=\pm a\]
We have the value of \[h\] from equation (i) as
\[h=k\sqrt{3}\]
By using the above conditions to equation (ii) and taking the positive sign first then we get
\[\begin{align}
& \Rightarrow \dfrac{\dfrac{k}{k\sqrt{3}}-\dfrac{k-2\sqrt{3}}{k\sqrt{3}}}{1+\dfrac{k-2\sqrt{3}}{3k}}=\sqrt{3} \\
& \Rightarrow \dfrac{k-k+2\sqrt{3}}{k\sqrt{3}}=\sqrt{3}\left( \dfrac{3k+k-2\sqrt{3}}{3k} \right) \\
& \Rightarrow 2=\dfrac{4k-2\sqrt{3}}{\sqrt{3}} \\
\end{align}\]
Now, by cross multiplying the terms in LHS and RHS then we get the value of \[k\] as
\[\begin{align}
& \Rightarrow 2\sqrt{3}=4k-2\sqrt{3} \\
& \Rightarrow 4k=4\sqrt{3} \\
& \Rightarrow k=\sqrt{3} \\
\end{align}\]
Now, by substituting the value of \[k\] in equation (i) then we get
\[\begin{align}
& \Rightarrow h=\left( \sqrt{3} \right)\sqrt{3} \\
& \Rightarrow h=3 \\
\end{align}\]
So, we can say that the third vertex is \[\left( 3,\sqrt{3} \right)\]
Now, let us take the negative sign in the equation (ii) then we get
\[\begin{align}
& \Rightarrow \dfrac{\dfrac{k}{k\sqrt{3}}-\dfrac{k-2\sqrt{3}}{k\sqrt{3}}}{1+\dfrac{k-2\sqrt{3}}{3k}}=-\sqrt{3} \\
& \Rightarrow \dfrac{k-k+2\sqrt{3}}{k\sqrt{3}}=-\sqrt{3}\left( \dfrac{3k+k-2\sqrt{3}}{3k} \right) \\
& \Rightarrow 2=-\left( \dfrac{4k-2\sqrt{3}}{\sqrt{3}} \right) \\
\end{align}\]
Now, by cross multiplying the terms in LHS and RHS then we get the value of \[k\] as
\[\begin{align}
& \Rightarrow 2\sqrt{3}=-4k+2\sqrt{3} \\
& \Rightarrow 4k=0 \\
& \Rightarrow k=0 \\
\end{align}\]
Now, by substituting the value of \[k\] in equation (i) then we get
\[\begin{align}
& \Rightarrow h=\left( 0 \right)\sqrt{3} \\
& \Rightarrow h=0 \\
\end{align}\]
Here, we can see that the vertex we get is \[\left( 0,0 \right)\] which is already given.
Therefore, we can conclude that the third vertex of the given equilateral triangle is \[\left( 3,\sqrt{3} \right)\]
Note:
We have a shortcut for solving this problem.
Let us take the rough figure of the given triangle as

Here, we can see that the value of \[h\] is the height of the triangle and \[k\] is half of side AB
Let us find the distance AB
We know that the distance formula if two points \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\] is given as
\[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
By using the above formula we get the distance AB as
\[\begin{align}
& \Rightarrow AB=\sqrt{{{\left( 2\sqrt{3}-0 \right)}^{2}}+{{\left( 0-0 \right)}^{2}}} \\
& \Rightarrow AB=2\sqrt{3} \\
\end{align}\]
Now, let us find the value of \[k\] which is half of AB
By using the above condition we get
\[\begin{align}
& \Rightarrow k=\dfrac{2\sqrt{3}}{2} \\
& \Rightarrow k=\sqrt{3} \\
\end{align}\]
We know that the height of equilateral triangle of side \[a\] is given as
\[height=\dfrac{\sqrt{3}}{2}a\]
By using the above formula we get the value of \[h\] as
\[\begin{align}
& \Rightarrow h=\dfrac{\sqrt{3}}{2}\left( 2\sqrt{3} \right) \\
& \Rightarrow h=3 \\
\end{align}\]
Therefore, we can conclude that the third vertex of the given equilateral triangle is \[\left( 3,\sqrt{3} \right)\]
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




