Question

If two triangles $\Delta DEF\sim \Delta PQR$. If 2DE = 3PQ, QR = 8 and DF = 6 then find EF and PR?

Answer 1

Hint: Use the similarity criteria that the ratios of the corresponding sides of similar triangles are equal and write the relation $\dfrac{DE}{PQ}=\dfrac{EF}{QR}=\dfrac{DF}{PR}$. Substitute the values of sides given and find the values of unknown sides using the cross multiplication. To find the ratio of DE and PQ divide both the sides of the relation 2DE = 3PQ by PQ.

Complete step by step answer:
Here we are provided with two triangles DEF and PQR such that they are similar. Also we have the relations and values 2DE = 3PQ, QR = 8 and DF = 6. We are asked to find the values of sides EF and PR. Let us draw a diagram for better understanding.

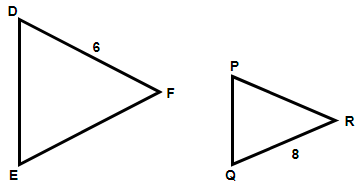
Now, we know that the ratios of the corresponding sides of similar triangles are equal so for the triangles $\Delta DEF\sim \Delta PQR$ we can write the relation $\dfrac{DE}{PQ}=\dfrac{EF}{QR}=\dfrac{DF}{PR}$. We have 2DE = 3PQ, so dividing both the sides with PQ we get,
$\begin{align}
  & \Rightarrow 2\times \dfrac{DE}{PQ}=3 \\
 & \Rightarrow \dfrac{DE}{PQ}=\dfrac{3}{2} \\
\end{align}$
Substituting the other ratios and values of the sides we get,
$\begin{align}
  & \Rightarrow \dfrac{EF}{QR}=\dfrac{DF}{PR}=\dfrac{3}{2} \\
 & \Rightarrow \dfrac{EF}{8}=\dfrac{6}{PR}=\dfrac{3}{2} \\
\end{align}$
(1) Considering the relation $\dfrac{EF}{8}=\dfrac{3}{2}$ we get,
$\begin{align}
  & \Rightarrow EF=\dfrac{3}{2}\times 8 \\
 & \therefore EF=12 \\
\end{align}$
(2) Considering the relation $\dfrac{6}{PR}=\dfrac{3}{2}$ we get,
$\begin{align}
  & \Rightarrow PR=\dfrac{2}{3}\times 6 \\
 & \therefore PR=4 \\
\end{align}$
Hence, the length of the sides EF and PR are 12 and 4 respectively.

Note: Note that in similarity of two triangles the ratios of their corresponding sides are equal and in congruency the corresponding sides of the triangles are equal. If two triangles are congruent then they must be similar but the converse need not to be true. You must remember the difference between similarity and congruence and their certain criteria also.