Question

If two straight lines intersect each other, prove that the ray opposite the bisector of one of the angles thus formed bisect the vertically opposite angle.

Answer 1

Hint:In this type of question first we draw the figure with given information by letting the rays name. Then, using properties of geometry angles, vertically opposite angle and angle bisector proving the ray opposite the bisector of one of the angles thus formed bisect the vertically opposite angle.

Complete step-by-step answer:
Given: Two straight lines intersect each other.
Let AB and CD are straight lines which intersect at point O. OP is the bisector of $\angle {\text{AOC}}$.
Now, extend the OP to Q.
 

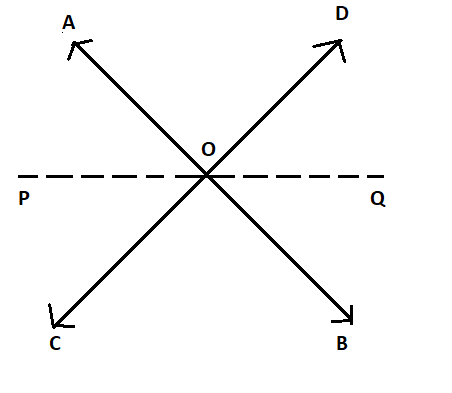
We have to prove OQ is the bisector of $\angle {\text{BOD}}$.
We know, AB, CD and PQ are the straight lines which intersect at point O.
Now,
$
   \Rightarrow \angle {\text{AOP = }}\angle {\text{BOQ (vertically opposite angles) eq}}{\text{.1}} \\
   \Rightarrow \angle {\text{COP = }}\angle {\text{DOQ (vertically opposite angles) eq}}{\text{.2 }} \\
   \Rightarrow \angle {\text{AOP = }}\angle {\text{COP (OP is the bisector of }}\angle {\text{AOC) eq}}{\text{.3 }} \\
$
From eq.1, eq.2 and eq.3, we get
$\angle {\text{BOQ = }}\angle {\text{DOQ}}$
Therefore, the ray opposite to the bisector of one of the angles thus formed bisects the vertically opposite angle.
Hence proved.

Note: Whenever you get this type of question the key concept to solve this is to learn the concept of angle bisector which is a line or line segment that divides an angle into two equal parts. And the concept of vertically opposite angles which states that in a pair of intersecting lines the vertically opposite angles are equal.