Question

If two straight lines are given by
\[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\text{ and }{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\]
Then find the angle between two lines.
(a) \[{{\tan }^{-1}}\dfrac{{{a}_{1}}{{b}_{2}}+{{a}_{2}}{{b}_{1}}}{{{a}_{1}}{{a}_{2}}-{{b}_{1}}{{b}_{2}}}\]
(b) \[{{\cot }^{-1}}\dfrac{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\]
(c) \[{{\cot }^{-1}}\dfrac{{{a}_{1}}{{b}_{1}}-{{a}_{2}}{{b}_{2}}}{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}}\]
(d) \[{{\tan }^{-1}}\dfrac{{{a}_{1}}{{b}_{1}}-{{a}_{2}}{{b}_{2}}}{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}}\]

Answer 1

Hint: Take the slopes of lines into account and apply plain geometry conditions used in triangles on the triangle formed by both the lines and X-axis. Use the formula below and find slopes of lines. After that use the condition in triangles, sum of any two interior angles is equal to the exterior angle made at third vertex and find relation between the angles. Now by applying tan you can find tan of the required angle in terms of slope. We know that if a line equation is ax + by + c = 0 , then its slope is given by:
\[m=-\dfrac{a}{b}\]

Complete step-by-step answer:
So as said above we will take the triangle formed by both the lines and X-axis.
Let the angles made by lines with the X-axis are marked as shown in the image.

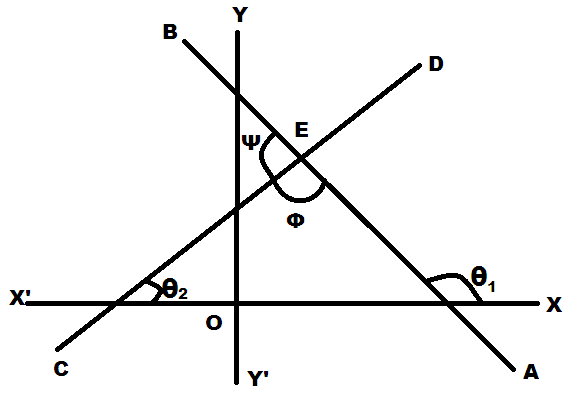
Let AB be the first line and CD be the second line,
 \[AB\equiv {{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\text{ and CD}\equiv {{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\]
From the image we can see the angle made by AB with X-axis, apply the slope condition:
\[\tan (\text{Angle made by line at X-axis})=\text{slope = m}\]
By applying above condition on AB and CD, we get:
\[\begin{align}
  & \tan \left( {{\theta }_{1}} \right)={{m}_{1}}.....\left( 1 \right) \\
 & \tan \left( {{\theta }_{2}} \right)={{m}_{2}}.....\left( 2 \right) \\
\end{align}\]
We know that if a line equation is ax + by + c = 0 , then its slope is given by:
\[m=-\dfrac{a}{b}\]
By applying above condition on AB and CD, we get:
\[\begin{align}
  & {{m}_{1}}=-\dfrac{{{a}_{1}}}{{{b}_{1}}}.....\left( 3 \right) \\
 & {{m}_{2}}=-\dfrac{{{a}_{2}}}{{{b}_{2}}}.....\left( 4 \right) \\
\end{align}\]
By substituting equation (3) and equation (4) in equation (1) and equation (2), we get:
\[\begin{align}
  & \tan {{\theta }_{1}}=-\dfrac{{{a}_{1}}}{{{b}_{1}}}.....\left( 5 \right) \\
 & \tan {{\theta }_{2}}=-\dfrac{{{a}_{2}}}{{{b}_{2}}}.....\left( 6 \right) \\
\end{align}\]
By plane geometry, condition of triangle:
Sum of any two interior angles is equal to the exterior angle made at the third vertex.
Applying above condition here, we get:
\[{{\theta }_{2}}+\phi ={{\theta }_{1}}\]
By simplifying, we get:
\[\phi ={{\theta }_{1}}-{{\theta }_{2}}\]
By applying tan on both sides, we get:
\[\tan \phi =\tan \left( {{\theta }_{1}}-{{\theta }_{2}} \right)\]
We know the formula:
\[\tan \left( A-B \right)=\dfrac{\tan A-\tan B}{1+\tan A\tan B}\]
By applying above formula, we get:
\[\tan \phi =\dfrac{\tan {{\theta }_{1}}-\tan {{\theta }_{2}}}{1+\left( \tan {{\theta }_{1}}.\tan {{\theta }_{2}} \right)}.....(7)\]
Now by substituting equation (5) and equation (6) in equation (7), we get:
\[\tan \phi =\dfrac{-\dfrac{{{a}_{1}}}{{{b}_{1}}}-\left( -\dfrac{{{a}_{2}}}{{{b}_{2}}} \right)}{1+\left( \left( -\dfrac{{{a}_{1}}}{{{b}_{1}}} \right).\left( -\dfrac{{{a}_{2}}}{{{b}_{2}}} \right) \right)}\]
By simplifying, we get:
\[\tan \phi =\dfrac{-\dfrac{{{a}_{1}}}{{{b}_{1}}}+\dfrac{{{a}_{2}}}{{{b}_{2}}}}{1+\left( \dfrac{{{a}_{1}}{{a}_{2}}}{{{b}_{1}}{{b}_{2}}} \right)}\]
By adding fractions and simplifying more, we get:
\[\begin{align}
  & \tan \phi =\dfrac{\dfrac{{{a}_{2}}{{b}_{1}}-{{a}_{1}}{{b}_{2}}}{{{b}_{1}}{{b}_{2}}}}{\dfrac{{{b}_{1}}{{b}_{2}}+{{a}_{1}}{{a}_{2}}}{{{b}_{1}}{{b}_{2}}}} \\
 & \tan \phi =\dfrac{{{a}_{2}}{{b}_{1}}-{{a}_{1}}{{b}_{2}}}{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}}.....\left( 8 \right) \\
 & \\
\end{align}\]
This doesn’t match with any options. So we need to find cotangent.
We know:
\[\cot \theta =\dfrac{1}{\tan \theta }\]
By applying this on equation (8), we get:
\[\,\cot \phi =\dfrac{1}{\dfrac{{{a}_{2}}{{b}_{1}}-{{a}_{1}}{{b}_{2}}}{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}}}=\dfrac{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}}{{{a}_{2}}{{b}_{1}}-{{a}_{1}}{{b}_{2}}}.....\left( 9 \right)\]
By equation (9), we get:
\[\phi ={{\cot }^{-1}}\,\dfrac{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}}{{{a}_{2}}{{b}_{1}}-{{a}_{1}}{{b}_{2}}}\]
\[\therefore \]The angle made by lines
\[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\text{ and }{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\Rightarrow {{\cot }^{-1}}\,\dfrac{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}}{{{a}_{2}}{{b}_{1}}-{{a}_{1}}{{b}_{2}}}\]
So, option (b) is the correct answer.

Note: Don’t confuse X-axis and Y-axis take the angles made by X-axis only.
Take the exterior angle equation such that it involves the angle between two lines because we need to find that.
Use the angular bisector concept as an alternative method.