Question

If two sides and a median bisecting the third side of a triangle are respectively proportional to the corresponding sides and the median of another triangle, then two triangles are similar.
A.${\text{True}}$
B. ${\text{False}}$

Answer 1

Hint: In this question ,we will solve this by applying some characteristic properties of similar triangles like SSS-similarity, SAS-similarity etc.

Complete step-by-step answer:
Let us take two triangles $\Delta $$ABC$ and $\Delta $$PQR$ in which $AL$ and $PM$ are the medians such that,
$\dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} = \dfrac{{AL}}{{PM}}$

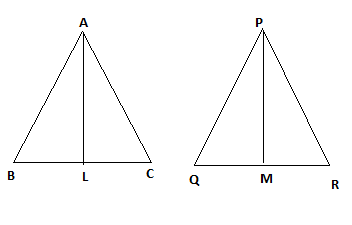
To prove :
$\Delta ABC \sim \Delta PQR$
Proof:
$\dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} = \dfrac{{AL}}{{PM}}$ [ Given ]
As we know that a median bisects a side in two equal parts.
$ \Rightarrow BL = LC$ and $QM = MR$
$ \Rightarrow BC = 2BL$ and $QR = 2QM$
$\therefore $$\dfrac{{AB}}{{PQ}} = \dfrac{{2BL}}{{2QM}} = \dfrac{{AL}}{{PM}}$
$ \Rightarrow $$\dfrac{{AB}}{{PQ}} = \dfrac{{BL}}{{QM}} = \dfrac{{AL}}{{PM}}$
$ \Rightarrow \Delta ABC \sim \Delta PQR$ [ By SSS-similarity test ]
$ \Rightarrow \angle B = \angle Q$ [ C.P.C.T ]
Now, In $\Delta ABC \sim \Delta PQR$ , we have
$ \Rightarrow \dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}}$
$\therefore $ and
 $\Delta ABC \sim \Delta PQR$ [ by SAS-similarity test ]

Note: In these types of questions,first we have to identify what is given in the question and then what we have to prove and then solve them by using the different characteristics properties of similar triangles such as SAS criteria or SSS criteria.