Question

If two parallel chords of a circle, having diameter 4 units, lie on the opposite sides of the centre and subtend angles \[{{\cos }^{-1}}\left( \dfrac{1}{7} \right)\] and ${{\sec }^{-1}}\left( 7 \right)$ at the centre respectively, then the distance between these chords, is:
(a) $\dfrac{8}{\sqrt{7}}$
(b) $\dfrac{4}{\sqrt{7}}$
(c) $\dfrac{8}{7}$
(d) $\dfrac{16}{7}$

Answer 1

Hint: To solve this question, we will first draw the figure. In the figure, we will construct a perpendicular from the centre of the circle to the chords. The angle subtended by the chords is given. We know that the diameter is 4, thus the distance of the centre of the circle with the end of the chord will be equal to radius, i.e. half the diameter. With the angle and the radius, we will use trigonometric ratios to find the perpendicular distances. Once we get the lengths of the perpendiculars, we will add the lengths to find the distance between the chords.

Complete step by step answer:
To begin with, we draw the circle with centre O. Let AB and CD be the chords on the opposite sides of the centre of the circle. Let E be the point on AB such that OE is perpendicular to AB and F be the point on CD such that OF is perpendicular to CD.

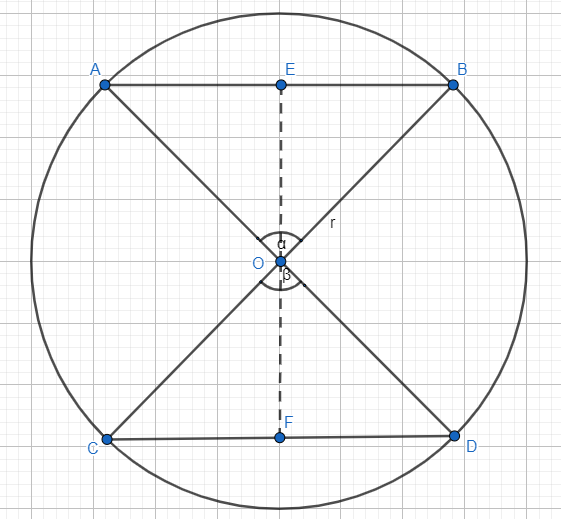
Let the angle subtended by AB = angle AOB be $\alpha $ and that subtended by CD = angle COD be $\beta $.
Thus, $\alpha ={{\cos }^{-1}}\left( \dfrac{1}{7} \right)$ and $\beta ={{\sec }^{-1}}\left( 7 \right)$.
But we know that $\alpha =\beta $, since they are vertically opposite angle.
This means OE = OF. Thus, the distance between the chords is EF = 2OE = 2OF.
Since OB = OA, the triangle OAB is an isosceles triangle.
Now, we know that in an isosceles triangle, the perpendicular drawn is also the angle bisector. Therefore, angle EOB is $\dfrac{\alpha }{2}$.
Now, if $\alpha ={{\cos }^{-1}}\left( \dfrac{1}{7} \right)$, $\cos \alpha =\dfrac{1}{7}$
From trigonometric ratios of half angles, we know that $\cos \alpha =2{{\cos }^{2}}\dfrac{\alpha }{2}-1$.
$\begin{align}
  & \Rightarrow 2{{\cos }^{2}}\dfrac{\alpha }{2}-1=\dfrac{1}{7} \\
 & \Rightarrow 2{{\cos }^{2}}\dfrac{\alpha }{2}=\dfrac{1}{7}+1 \\
 & \Rightarrow 2{{\cos }^{2}}\dfrac{\alpha }{2}=\dfrac{8}{7} \\
 & \Rightarrow \cos \dfrac{\alpha }{2}=\dfrac{2}{\sqrt{7}} \\
\end{align}$
But from the diagram and definition of cosine from trigonometry, we know that $\cos \dfrac{\alpha }{2}=\dfrac{OE}{OB}$ .
$\begin{align}
  & \Rightarrow \dfrac{2}{\sqrt{7}}=\dfrac{OE}{2} \\
 & \Rightarrow OE=\dfrac{4}{\sqrt{7}} \\
\end{align}$
Therefore, the distance is twice that of OE = $2\times \dfrac{4}{\sqrt{7}}=\dfrac{8}{\sqrt{7}}$.

So, the correct answer is “Option A”.

Note: Another way to prove that $\alpha =\beta $ is the value of $\alpha ={{\cos }^{-1}}\left( \dfrac{1}{7} \right)$ and $\beta ={{\sec }^{-1}}\left( 7 \right)$. But we know that ${{\cos }^{-1}}x={{\sec }^{-1}}\left( \dfrac{1}{x} \right)$ . Thus $\beta =co{{s}^{-1}}\left( \dfrac{1}{7} \right)$. Thus $\alpha =\beta $.